Question

2．如图，已知动点A在反比例函数y=$\frac{2}{x}$（x＞0）图象上，AB⊥x轴于点B，AC⊥y轴于点C，延长CA到点D，使AD=$\frac{1}{2}$AB，延长BA到点E，使AE=$\frac{1}{2}$AC，直线DE分别交x、y轴于点P、Q，当$\frac{QE}{DP}$=$\frac{4}{9}$时，则△ACE与△ADB面积之和等于$\frac{13}{12}$．

Answer 1

分析 作DF⊥x轴于点F，EG⊥y轴于G，得到△QEG∽△PDF，于是得到$\frac{EG}{PF}$=$\frac{QE}{DP}$=$\frac{4}{9}$，设EG=4t，则PF=9t，然后根据△ADE∽△FPD，据此即可得到关于t的方程，求得t的值，进而求解．

解答 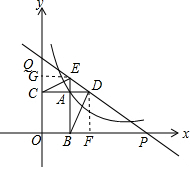解：作DF⊥x轴于点F，EG⊥y轴于G，
∴△QEG∽△DPF，
∴$\frac{EG}{PF}$=$\frac{QE}{DP}$=$\frac{4}{9}$，
设EG=4t，则PF=9t，
∴A（4t，$\frac{1}{2t}$），
∵AE=$\frac{1}{2}$AC，AD=$\frac{1}{2}$AB，
∴AE=2t，AD=$\frac{1}{4t}$，DF=$\frac{1}{2t}$，PF=9t，
∵△ADE∽△FPD，
∴AE：DF=AD：PF，即2t：$\frac{1}{2t}$=$\frac{1}{4t}$：9t，即t²=$\frac{1}{12}$，
△ACE与△ADB面积之和=$\frac{1}{2}$×2t×4t+$\frac{1}{2}$×$\frac{1}{4t}$×$\frac{1}{2t}$=$\frac{13}{12}$．
故答案为：$\frac{13}{12}$．

点评 本题考查了反比例函数综合题，涉及到从反比例函数y=$\frac{k}{x}$（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|，也考查了相似三角形的判定与性质．