��Ŀ����
10��ij����˶�Ա��ͬһ�����½����������������ʾ��| ����ܴ���n | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
| ���а��Ĵ���m | 9 | 16 | 41 | 88 | 168 | 429 | 861 |
| ���а���Ƶ�� $\frac{m}{n}$ | 0.9 | 0.8 | 0.82 | 0.88 | 0.84 | 0.858 | 0.861 |
��2�����ݱ��������˶�Ա���а��ĵ�Ƶ�ʵ�����ͳ��ͼ��
��3���۲컭��������ͳ��ͼ�����а��ĵ�Ƶ�ʵı仯��ʲô���ɣ�
���� ��1��Ƶ����ָÿ��������ֵĴ������ܴ����ı�ֵ�����߰ٷֱȣ�����Ƶ��=Ƶ��������������
��2�����ݱ����е�Ƶ�ʣ��������˶�Ա���а��ĵ�Ƶ�ʵ�����ͳ��ͼ��
��3������Ƶ�ʵ����壬����Ƶ�ʵ�����ͳ��ͼ�ı仯���ƣ��ó����а��ĵ�Ƶ�ʵĽ���ֵ��
��� �⣺��1��$\frac{9}{10}$=0.9��$\frac{16}{20}$=0.8��$\frac{41}{50}$=0.82��$\frac{88}{100}$=0.88��$\frac{168}{200}$=0.84��$\frac{429}{500}$=0.858��$\frac{861}{1000}$=0.861��
�ʴ�Ϊ��0.9��0.8��0.82��0.88��0.84��0.858��0.861��
��2����ͼ��ʾ���˶�Ա���а��ĵ�Ƶ�ʵ�����ͳ��ͼΪ��
��3����������ͳ��ͼ���ɵû��а��ĵ�Ƶ�ʽӽ���0.86��
���� ������Ҫ����������Ƶ�ʹ��Ƹ����Լ�Ƶ������ȷ����Ƶ�ʵ������ǽ���ؼ���

��ϰ��ϵ�д�
 ������ϵ�д�
������ϵ�д�
�����Ŀ
1�� ѡ����չ��������ͼ��ʾ��ͼ����ͬ���ǣ�������
ѡ����չ��������ͼ��ʾ��ͼ����ͬ���ǣ�������
 ѡ����չ��������ͼ��ʾ��ͼ����ͬ���ǣ�������
ѡ����չ��������ͼ��ʾ��ͼ����ͬ���ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
18�����з����в��ܻ�������С�����ǣ�������
| A�� | $\frac{9}{16}$ | B�� | $\frac{3}{8}$ | C�� | $\frac{5}{18}$ | D�� | $\frac{7}{50}$ |
15����0��a��b��$\sqrt{\frac{a}{b}}$+$\sqrt{\frac{b}{a}}$=$\sqrt{6}$����$\frac{a-b}{a+b}$��ֵ�ǣ�������
| A�� | $\frac{\sqrt{3}}{3}$ | B�� | -$\sqrt{3}$ | C�� | -$\frac{\sqrt{6}}{2}$ | D�� | -$\frac{\sqrt{3}}{3}$ |
20��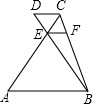 ��ͼ��AB��DC��AC��BD ���ڵ�E��EF��DC��BC�ڵ�F��CE=5��CF=4��AE=BC����$\frac{DC}{AB}$���ڣ�������
��ͼ��AB��DC��AC��BD ���ڵ�E��EF��DC��BC�ڵ�F��CE=5��CF=4��AE=BC����$\frac{DC}{AB}$���ڣ�������
 ��ͼ��AB��DC��AC��BD ���ڵ�E��EF��DC��BC�ڵ�F��CE=5��CF=4��AE=BC����$\frac{DC}{AB}$���ڣ�������
��ͼ��AB��DC��AC��BD ���ڵ�E��EF��DC��BC�ڵ�F��CE=5��CF=4��AE=BC����$\frac{DC}{AB}$���ڣ�������| A�� | $\frac{2}{3}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{3}{5}$ |
 ��ͼ����������ABCD�У�AB=4��BD�ǶԽ��ߣ�����DCB����D����ʱ����ת����90�㣼����180�㣩���õ���DEF������BF��CE�ཻ��G�㣬EG=1����BF=$\sqrt{62}$+$\sqrt{2}$��
��ͼ����������ABCD�У�AB=4��BD�ǶԽ��ߣ�����DCB����D����ʱ����ת����90�㣼����180�㣩���õ���DEF������BF��CE�ཻ��G�㣬EG=1����BF=$\sqrt{62}$+$\sqrt{2}$�� ��ͼ����֪����A�ڷ���������y=$\frac{2}{x}$��x��0��ͼ���ϣ�AB��x���ڵ�B��AC��y���ڵ�C���ӳ�CA����D��ʹAD=$\frac{1}{2}$AB���ӳ�BA����E��ʹAE=$\frac{1}{2}$AC��ֱ��DE�ֱ�x��y���ڵ�P��Q����$\frac{QE}{DP}$=$\frac{4}{9}$ʱ�����ACE���ADB���֮�͵���$\frac{13}{12}$��
��ͼ����֪����A�ڷ���������y=$\frac{2}{x}$��x��0��ͼ���ϣ�AB��x���ڵ�B��AC��y���ڵ�C���ӳ�CA����D��ʹAD=$\frac{1}{2}$AB���ӳ�BA����E��ʹAE=$\frac{1}{2}$AC��ֱ��DE�ֱ�x��y���ڵ�P��Q����$\frac{QE}{DP}$=$\frac{4}{9}$ʱ�����ACE���ADB���֮�͵���$\frac{13}{12}$��