题目内容
19．小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形，她对折了（ ）| A． | 1次 | B． | 2次 | C． | 3次 | D． | 4次 |
分析 由折叠得出四个角相等的四边形是矩形，再由一组邻边相等，即可得出四边形是正方形．
解答 解：小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形，她对折了2次；理由如下：
小红把原丝巾对折1次（共2层），2组邻角相等，且一组对边相等；
将丝巾展开后沿对角线对折，则对角相等，两组邻边长度相等，所以4个角相等，且4条边相等．则这个四边形是正方形．
故选：B．
点评 本题考查了翻折变换的性质、矩形的判定、正方形的判定；熟练掌握翻折变换和正方形的判定是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
11．下列计算正确的是（ ）
| A． | （a2b）2=a2b2 | B． | a6÷a2=a3 | C． | （3xy2）2=6x2y4 | D． | （-m）7÷（-m）2=-m5 |
7．-2016的倒数是（ ）
| A． | -2016 | B． | -$\frac{1}{2016}$ | C． | $\frac{1}{2016}$ | D． | 2016 |
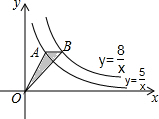如图，点A在双曲线y=$\frac{5}{x}$上，点B在双曲线y=$\frac{8}{x}$上，且AB∥x轴，则△OAB的面积等于$\frac{3}{2}$．
保护视力要求人写字时眼睛和笔端的距离应超过30cm，图1是一位同学的坐姿，把他的眼睛B，肘关节C和笔端A的位置关系抽象成图2的△ABC，已知BC=30cm，AC=22cm，∠ACB=53°，他的这种坐姿符合保护视力的要求吗？请说明理由．（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3）
11．平面直角坐标系中，点P（-2，3）关于x轴对称的点的坐标为（ ）
| A． | （-2，-3） | B． | （2，-3） | C． | （-3，-2） | D． | （3，-2） |
