��Ŀ����
16�����Ķ����в��ϣ��ٽ���������⣮��1+2+22+23+24+��+2100�ĺͣ�
�⣺��S=1+2+22+23+24+��+2100����
����ʽ����ͬʱ����2���ã�
2S=2+22+23+24+25+��+2101������ ��
��-�٣���
2S-S=2101-1��
�� S=2101-1
����1+2+22+23+24+��+2100=2101-1
������
��1������1+2+22+23+��+22016�ĺͣ���д��������̣�
��2����1+32+34+36+38+��+32n�ĺͣ�����nΪ����������
��3����Sn=1+32+34+36+38+��+32n������nΪ������������˵����$\sqrt{\frac{8{S}_{2n}+1}{9}}$=$\frac{8{S}_{n}+1}{9}$��
���� ��1������������������Ŀ������ʽ�ӵ�ֵ��
��2��������Ŀ�е���Ϣ��������ʽ�ӱ��μ��ɽ���⣻
��3�����ݣ�2���еĽ���ֱ���Ҫ֤����ʽ�Ӽ��ɽ���⣮
��� �⣺��1��1+2+22+23+24+��+22016=22017-1��
��S=1+2+22+23+24+��+22016��
����ʽ����ͬʱ����2���ã�
2S=2+22+23+24+25+��+22017��
��-�٣���2S-S=22017-1���� S=22017-1��
����1+2+22+23+24+��+22016=22017-1��
��2����S=1+32+34+36+38+��+32n��
����ʽ����ͬʱ����32���ã�9S=32+34+36+38+��+32n+2��
��-�٣���9S-S=32n+2-1����S=$\frac{{3}^{2n+2}-1}{8}$��
��3���ɣ�2���ɵã�Sn=$\frac{{3}^{2n+2}-1}{8}$��S2n=$\frac{{3}^{4n+2}-1}{8}$��
��$\sqrt{\frac{8{S}_{2n}+1}{9}}=\sqrt{\frac{8��\frac{{3}^{4n+2}-1}{8}+1}{9}}$=$\sqrt{\frac{{3}^{4n+2}}{9}}$=$\frac{{3}^{2n+1}}{3}$��
$\frac{8{S}_{n}+1}{9}=\frac{8��\frac{{3}^{2n+2}-1}{8}+1}{9}=\frac{{3}^{2n+2}}{9}$=$\frac{{3}^{2n+1}}{3}$��
��$\sqrt{\frac{8{S}_{2n}+1}{9}}$=$\frac{8{S}_{n}+1}{9}$��
���� ���⿼��ʵ�������㣬����Ĺؼ�����ȷ���⣬�ҳ����ֵı仯�ص㣬��ȷʵ������ķ�����

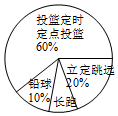 ij��ͬѧ��Ӧ�����������˶������٣����ÿ��������μ�����������ÿλͬѧ�ӳ��ܡ�Ǧ��������Զ������ʱ����Ͷ������ѡһ�������ѵ����ѵ�������˲�ѵ��������Ͷ�����Խ�����������ͳ�Ʊ�
ij��ͬѧ��Ӧ�����������˶������٣����ÿ��������μ�����������ÿλͬѧ�ӳ��ܡ�Ǧ��������Զ������ʱ����Ͷ������ѡһ�������ѵ����ѵ�������˲�ѵ��������Ͷ�����Խ�����������ͳ�Ʊ�| ������������ | 8 | 7 | 6 | 5 | 4 | 3 |
| ���� | 2 | 1 | 4 | 7 | 8 | 2 |
��1��ѵ��������ʱ����Ͷ���˾�������Ϊ���ٸ���
��2��ѡ����ѵ��������ռȫ�������İٷֱ���10%���ð��ͬѧ40�ˣ�
��3�����ݲ������ϣ��μ�����ʱ����Ͷ����ѧ��ѵ�����ѵ��ǰ���˾�����������25%����μ�ѵ��֮ǰ���˾���������
| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� | $\root{3}{9}$ | B�� | ��$\root{3}{3}$ | C�� | 3 | D�� | ��$\root{3}{9}$ |
 ��ͼ����֪��AB=CD��BF��AC��DE��AC��AE=CF����֤��AB��CD��
��ͼ����֪��AB=CD��BF��AC��DE��AC��AE=CF����֤��AB��CD��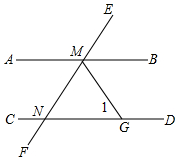 ��ͼ��AB��CD��EF�ֱ�AB��CD��M��N����END=50�㣬��BMF�Ľ�ƽ����MG��CD�ڵ�G�����1�Ķ�����
��ͼ��AB��CD��EF�ֱ�AB��CD��M��N����END=50�㣬��BMF�Ľ�ƽ����MG��CD�ڵ�G�����1�Ķ�����