题目内容
13．已知一等腰三角形的周长为12$\sqrt{5}$，其中一边的长为2$\sqrt{5}$，则这个等腰三角形的腰长为5$\sqrt{5}$．分析 直接利用当腰长为2$\sqrt{5}$或底边长为2$\sqrt{5}$，分类讨论得出答案．
解答 解：当腰长为2$\sqrt{5}$，则底边长为：12$\sqrt{5}$-4$\sqrt{5}$=8$\sqrt{5}$，
此时2$\sqrt{5}$+2$\sqrt{5}$＜8$\sqrt{5}$，无法构成三角形，
当底边长为2$\sqrt{5}$，故腰长为：（12$\sqrt{5}$-2$\sqrt{5}$）÷2=5$\sqrt{5}$，
故答案为：5$\sqrt{5}$．
点评 此题主要考查了二次根式的应用以及等腰三角形的性质，正确分类讨论是解题关键．
练习册系列答案
相关题目
如图，在网格图中，每个小正方形的顶点叫做格点，以格点为顶点的三角形叫做格点三角形，且每个小正方形的边长均为1，三角形ABC为一格点三角形，认真观察图形，请你求出三角形ABC的面积．
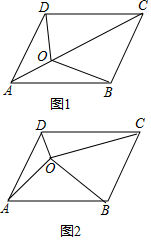我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形．
如图，在四边形ABCD中，∠ABC=60°，∠BAD=150°，AB边的中点，连接EC、ED，得到△EDC是等边三角形．取BF=AB并连接AF，若CF=3，则AF=6．