题目内容
11.解不等式组$\left\{\begin{array}{l}{\frac{1}{2}+\frac{2x}{3}≤-\frac{x}{2}+\frac{5}{3}}\\{3(x-1)<x-5}\end{array}\right.$,并把解集表示在数轴上.分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{\frac{1}{2}+\frac{2x}{3}≤-\frac{x}{2}+\frac{5}{3}①}\\{3(x-1)<x-5②}\end{array}\right.$
∵解不等式①得:x≤1,
解不等式②得:x<-1,
∴不等式组的解集为x<-1,
故在数轴上表示不等式组的解集为: .
.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集的应用,能根据不等式的解集找出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
6.下列说法中:
①两个位似图形一定相似;
②邻补角的平分线互相垂直;
③一组数据的极差、方差越小,该组数据就越稳定;
④在△ABC中,如果∠A:∠B:∠C=3:4:5,那么∠C=90°,
其中正确的个数是( )
①两个位似图形一定相似;
②邻补角的平分线互相垂直;
③一组数据的极差、方差越小,该组数据就越稳定;
④在△ABC中,如果∠A:∠B:∠C=3:4:5,那么∠C=90°,
其中正确的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.点A(a,b)在第二象限,到x轴的距离是2,到y轴距离是3,则点A坐标为( )
| A. | (-2,3) | B. | (-3,-2) | C. | (-3,2) | D. | (2,3) |
 用
用 表示三种不同的物体,现放在天平上比较两次,情况如图所示,那么,这三种物体质量的大小关系应为a=b<c.
表示三种不同的物体,现放在天平上比较两次,情况如图所示,那么,这三种物体质量的大小关系应为a=b<c.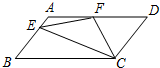 如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论中一定成立的个数是( )
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论中一定成立的个数是( )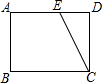 如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为3或6.
如图,在矩形纸片ABCD中,已知AB=6,BC=8,E是边AD上的点,以CE为折痕折叠纸片,使点D落在点F处,连接FC,当△AEF为直角三角形时,DE的长为3或6.