题目内容
9.解方程:(1)x2-3x+2=0;
(2)x2-6x+4=0.
分析 (1)把方程左边分解得到(x-1)(x-2)=0,则原方程可化为x-1=0或x-2=0,然后解两个一次方程即可.
(2)把常数项移到右边,两边加上一次项系数一半的平方,左边配成完全平方的形式,再用直接开平方求出方程的根.
解答 解:(1)x2-3x+2=0;
分解因式得:(x-1)(x-2)=0,
∴x-1=0,x-2=0,
∴x1=1,x2=2.
(2)x2-6x+4=0.
x2-6x=-4
x2-6x+9=5
(x-3)2=5
x-3=±$\sqrt{5}$
∴x=3$±\sqrt{5}$
∴x1=3$+\sqrt{5}$,x2=3-$\sqrt{5}$.
点评 本题考查了解一元二次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
19.为了参加我市召开的“生态文明贵阳国际论谈2013年年会”开幕式活动,某校准备从八年级的四个班中选出一个班的学生组建舞蹈队,要求选出的学生身高较为整齐,且平均身高为1.6m,通过测量各班学生的身高,计算得到的数据如下表所示,学校应选择( )
| 学生平均身高(单位:m) | 标准差 | |
| 八(1)班 | 1.57 | 0.3 |
| 八(2)班 | 1.57 | 0.7 |
| 八(3)班 | 1.60 | 0.3 |
| 八(4)班 | 1.60 | 0.7 |
| A. | 八(1)班 | B. | 八(2)班 | C. | 八(3)班 | D. | 八(4)班 |
 已知,FA,DF分别平分∠EAC,∠CDB,试探索∠C,∠F,∠B之间的关系.
已知,FA,DF分别平分∠EAC,∠CDB,试探索∠C,∠F,∠B之间的关系.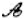 线”,点P为“
线”,点P为“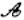 点”.
点”.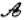 点”的坐标;
点”的坐标;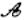 线”,并说明理由;
线”,并说明理由; 线”,求k的取值范围.
线”,求k的取值范围. 点”的⊙C的“
点”的⊙C的“ 线”,求r的值.
线”,求r的值.