题目内容
3.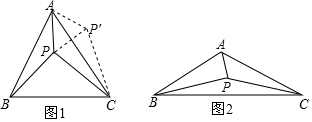 在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=$\frac{α}{2}$,连接PB,试探究PA、PB、PC满足的等量关系.
在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=$\frac{α}{2}$,连接PB,试探究PA、PB、PC满足的等量关系.(1)当α=60°时,将△ABP绕点A逆时针旋转60°得到△ACP′,连接PP′,如图1所示.由△ABP≌△ACP′可以证得△APP′是等边三角形,再由∠PAC+∠PCA=30°可得∠APC的大小为150度,进而得到△CPP′是直角三角形,这样可以得到PA、PB、PC满足的等量关系为PA2+PC2=PB2;
(2)如图2,当α=120°时,参考(1)中的方法,探究PA、PB、PC满足的等量关系,并给出证明;
(3)PA、PB、PC满足的等量关系为4PA2•sin2$\frac{α}{2}$+PC2=PB2.
分析 (1)根据旋转变换的性质得到△PAP′为等边三角形,得到∠P′PC=90°,根据勾股定理解答即可;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,作AD⊥PP′于D,根据余弦的定义得到PP′=$\sqrt{3}$PA,根据勾股定理解答即可;
(3)与(2)类似,根据旋转变换的性质、勾股定理和余弦、正弦的关系计算即可.
解答 解:(1)∵△ABP≌△ACP′,
∴AP=AP′,
由旋转变换的性质可知,∠PAP′=60°,P′C=PB,
∴△PAP′为等边三角形,
∴∠APP′=60°,
∵∠PAC+∠PCA=$\frac{60°}{2}$=30°,
∴∠APC=150°,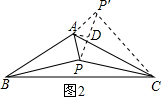
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∴PA2+PC2=PB2,
故答案为:150,PA2+PC2=PB2;
(2)如图2,作将△ABP绕点A逆时针旋转120°得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=120°,P′C=PB,
∴∠APP′=30°,
∵∵∠PAC+∠PCA=$\frac{120°}{2}$=60°,
∴∠APC=120°,
∴∠P′PC=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=30°,
∴PD=$\frac{\sqrt{3}}{2}$PA,
∴PP′=$\sqrt{3}$PA,
∴3PA2+PC2=PB2;
(3)如图2,与(2)的方法类似,
作将△ABP绕点A逆时针旋转α得到△ACP′,连接PP′,
作AD⊥PP′于D,
由旋转变换的性质可知,∠PAP′=α,P′C=PB,
∴∠APP′=90°-$\frac{α}{2}$,
∵∵∠PAC+∠PCA=$\frac{α}{2}$,
∴∠APC=180°-$\frac{α}{2}$,
∴∠P′PC=(180°-$\frac{α}{2}$)-(90°-$\frac{α}{2}$)=90°,
∴PP′2+PC2=P′C2,
∵∠APP′=90°-$\frac{α}{2}$,
∴PD=PA•cos(90°-$\frac{α}{2}$)=PA•sin$\frac{α}{2}$,
∴PP′=2PA•sin$\frac{α}{2}$,
∴4PA2sin2$\frac{α}{2}$+PC2=PB2,
故答案为:4PA2sin2$\frac{α}{2}$+PC2=PB2.
点评 本题考查的是旋转变换的性质、等边三角形的性质、勾股定理的应用,掌握等边三角形的性质、旋转变换的性质、灵活运用类比思想是解题的关键.

 字词句段篇系列答案
字词句段篇系列答案 将正△ABC的各边四等分,如图,则图中全等的三角形共有( )对.
将正△ABC的各边四等分,如图,则图中全等的三角形共有( )对.| A. | 100 | B. | 121 | C. | 144 | D. | 169 |
 已知A、B两地相距40km,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑自行车,图中CD、OE分别表示甲、乙离开A地的路程y(km)与时间x(h)的函数关系的图象,结合图象解答下列问题.
已知A、B两地相距40km,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑自行车,图中CD、OE分别表示甲、乙离开A地的路程y(km)与时间x(h)的函数关系的图象,结合图象解答下列问题. 已知:如图,△ABC内接于⊙O,∠C=45°,AB=2,求⊙O的半径.
已知:如图,△ABC内接于⊙O,∠C=45°,AB=2,求⊙O的半径.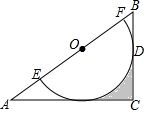 如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于E,F两点,BC切⊙O于点D,且CD=$\frac{1}{2}$EF=1.
如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于E,F两点,BC切⊙O于点D,且CD=$\frac{1}{2}$EF=1.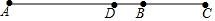 如图,已知线段AB的长为a,延长线段AB至点C,使BC=$\frac{1}{2}$AB.
如图,已知线段AB的长为a,延长线段AB至点C,使BC=$\frac{1}{2}$AB.