题目内容
8.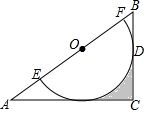 如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于E,F两点,BC切⊙O于点D,且CD=$\frac{1}{2}$EF=1.
如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于E,F两点,BC切⊙O于点D,且CD=$\frac{1}{2}$EF=1.(1)求证:⊙O与AC相切;
(2)求图中阴影部分的面积.
分析 (1)连接OD,过点O作OH⊥AC于点H,先根据题意得出四边形OHCD是矩形,进而可得出结论;
(2)直接根据S阴影=S正方形ODCH-S扇形ODH即可得出结论.
解答 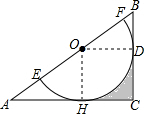 (1)证明:连接OD,过点O作OH⊥AC于点H,
(1)证明:连接OD,过点O作OH⊥AC于点H,
∵BC是⊙O的切线,
∴OD⊥BC.
∵∠C=90°,
∴∠OHC=∠ODC=∠C=90°,
∴四边形OHCD是矩形.
∵CD=$\frac{1}{2}$EF,
∴OH=$\frac{1}{2}$EF=OE.
∵OH⊥AC,
∴AC是⊙O的切线;
(2)解:∵OD=$\frac{1}{2}$EF=1,CD=1,∠DOH=90°,
∴S阴影=1×1-$\frac{90π×{1}^{2}}{360}$=1-$\frac{1}{4}$π.
点评 本题考查的是切线的判定与性质,熟知切线的判定定理是解答此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
16.二次函数y=ax2+bx+c的部分对应值如下表:
当x=-1时,对应的函数值y=-22.
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | -54 | -36 | -12 | -6 | -6 | -22 | … |
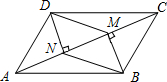 如图,AC是平行四边形ABCD的一条对角线,过点B作BM⊥AC于点M,多点D作DN⊥AC于点N,分别连接BN与DM,求证:BN=DM.
如图,AC是平行四边形ABCD的一条对角线,过点B作BM⊥AC于点M,多点D作DN⊥AC于点N,分别连接BN与DM,求证:BN=DM.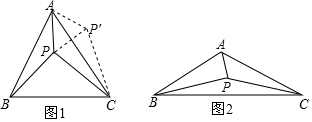 在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=$\frac{α}{2}$,连接PB,试探究PA、PB、PC满足的等量关系.
在△ABC中,AB=AC,∠BAC=α,点P是△ABC内一点,且∠PAC+∠PCA=$\frac{α}{2}$,连接PB,试探究PA、PB、PC满足的等量关系. 如图,抛物线y=a(x-1)2+k与x轴交于A、C两点,与y轴交于点B,点A、B的坐标分别为(-1,0)和(0,3).
如图,抛物线y=a(x-1)2+k与x轴交于A、C两点,与y轴交于点B,点A、B的坐标分别为(-1,0)和(0,3).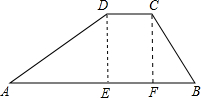 如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.
如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.