题目内容
11. 如图,MN是等边三角形ABC的一条对称轴,D为AC的中点,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD的度数是30°.
如图,MN是等边三角形ABC的一条对称轴,D为AC的中点,点P是直线MN上的一个动点,当PC+PD最小时,∠PCD的度数是30°.
分析 由于点C关于直线MN的对称点是B,所以当B、P、D三点在同一直线上时,PC+PD的值最小.
解答 解:由题意知,当B、P、D三点位于同一直线时,PC+PD取最小值,
连接BD交MN于P,
∵△ABC是等边三角形,D为AC的中点,
∴BD⊥AC,
∴PA=PC,
∴∠PCD=∠PAD=30°
故答案为:30°.
点评 此题考查了线路最短的问题,确定动点为何位置时,使PC+PD的值最小是关键.

练习册系列答案
相关题目
20.已知y是x的一次函数,函数y与自变量x的部分对应值如表,
点(x1,y1),(x2,y2)在该函数的图象上.若x1>x2,则y1<y2.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 10 | 8 | 6 | 4 | 2 | … |
1.对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 顶点坐标是(1,2) | C. | 对称轴是x=-1 | D. | 与x轴有两个交点 |
 如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD=∠C=45°,AB=8,CD=9,则AD的长为5.
如图,四边形ABCD,M为BC边的中点.若∠B=∠AMD=∠C=45°,AB=8,CD=9,则AD的长为5. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4),将△ABC绕着点B顺时针旋转90°后得到△A1BC1,请在图中画出△A1BC1,并求出线段BC旋转过程中所扫过的面积(结果保留π)
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4),将△ABC绕着点B顺时针旋转90°后得到△A1BC1,请在图中画出△A1BC1,并求出线段BC旋转过程中所扫过的面积(结果保留π)
 已知在同心圆中,大圆的弦AB切小圆于T,过T的直线交大圆于C、D,交小圆于E.
已知在同心圆中,大圆的弦AB切小圆于T,过T的直线交大圆于C、D,交小圆于E.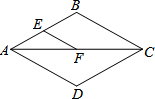 如图,AC是菱形ABCD的对角线,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是16.
如图,AC是菱形ABCD的对角线,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是16. 如图,E、C、F、C四点在一条直线上,EB=FC,∠A=∠D,再添一个条件就能证明△ABC≌△DEF,这个条件可以是∠ABC=∠E.(只写一个即可).
如图,E、C、F、C四点在一条直线上,EB=FC,∠A=∠D,再添一个条件就能证明△ABC≌△DEF,这个条件可以是∠ABC=∠E.(只写一个即可).