题目内容
16.已知α、β均为锐角,且满足$|{sinα-\frac{1}{2}}|+\sqrt{{{(tanβ-1)}^2}}=0$.计算:$2cosα-|{cosβ+\frac{{\sqrt{2}}}{2}}|+2\sqrt{1-{{sin}^2}β}-\sqrt{3}(tanα+1{)^0}$.
分析 由非负数的性质及特殊角的三角函数值求出α与β的度数,代入原式计算即可得到结果.
解答 解:由|sinα-$\frac{1}{2}$|+$\sqrt{(tanβ-1)^{2}}$=0,
得到sinα=$\frac{1}{2}$,tanβ=1,
∴α=30°,β=45°,
则原式=$\sqrt{3}$-$\sqrt{2}$+$\sqrt{2}$-$\sqrt{3}$=0.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.△ABC≌△DEF,A与D对应,B与E对应,∠A=32°,∠B=68°,则∠F为( )
| A. | 100° | B. | 80° | C. | 32° | D. | 68° |
1.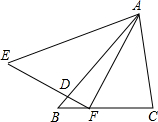 如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
 如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )
如图,在△ABC和△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.下列结论中正确的是( )①∠AFC=∠C;②DF=CF;③△ADE∽△FDB;④∠BFD=∠CAF.
| A. | 只有①③ | B. | 只有①④ | C. | 只有③④ | D. | 只有①③④ |
 某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.
某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.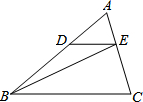 如图,在△ABC中,点D、E分别是AB、AC上的点,DE∥BC,S△ADE:S△BDE=2:3,若S△BEC=15,则S△ABC=( )
如图,在△ABC中,点D、E分别是AB、AC上的点,DE∥BC,S△ADE:S△BDE=2:3,若S△BEC=15,则S△ABC=( ) 如图,已知?ABCD中,AB=6,∠DAB=60°,AC平分∠DAB,E为AB的中点,点F是AC上一动点,求EF+BF的最小值.
如图,已知?ABCD中,AB=6,∠DAB=60°,AC平分∠DAB,E为AB的中点,点F是AC上一动点,求EF+BF的最小值.