题目内容
6. 某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.
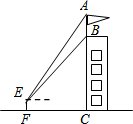
某公司研发一款新型的测角仪,这种测角仪能更精确的测量角度,减少误差.(1)如图,小明为了得到教学楼BC上旗杆AB的高度,用新型测角仪在与BC相距12m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,请你帮小明求出旗杆AB的高度.(结果精确到0.1m.参考数据:∠AGB=90°≈1.41,sin52°≈0.79,tan52°≈1.28)
(2)目前公司有100台机器,平均每台能生产400套,由于该仪器大受欢迎,工厂计划增加产量;但是由于机器故障,每台平均生产套数将减少1.25a%(20<a<30),要使生产总量增加10%,则机器台数需增加2.4a%,求a的值.
分析 (1)过E点作EH⊥BC于H点,在RT△BEH中利用三角函数求得BH的长,然后在直角△EAH中,利用三角函数求得AH的长,根据AB=AH-BH即可求解;
(2)根据机器的总生产量等于机器数与每台生产的产品数即可列方程求解.
解答 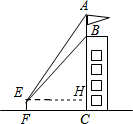 解:(1)过E点作EH⊥BC于H点,
解:(1)过E点作EH⊥BC于H点,
由题:∠AEH=52°,∠BEH=45°,EH=12m,
在RT△BEH中,∵∠BEH=45°
∴BH=EH=12m
在Rt△EAH中,AH=EH•tan52°=15.36m
∴AB=AH-BH≈3.4m
(2)由题意得:40000(1+10%)=400(1-1.25a%)•100(1+2.4a%),
解得:a1=25,a2=$\frac{40}{3}$.
∵20<a<30,
∴a=25.
答:a的值为25.
点评 本题考查了解直角三角形的应用和一元二次方程的应用,正确理解:机器的总生产量等于机器数与每台生产的产品数是关键.

练习册系列答案
相关题目
1.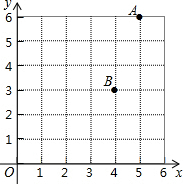 如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )
如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )
 如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )
如图是某市两个小区的大致位置示意图,图中点A表示的是茗茗家所居住的小区,点B表示的是茗茗奶奶家所居住的小区,按照先列后行的顺序,点A和点B所在的位置可以表示为( )| A. | (6,5)和(3,4) | B. | (5,6)和(3,4) | C. | (6,5)和(4,3) | D. | (5,6)和(4,3) |
15.下列不是三棱柱展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
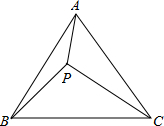 已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.
已知,如图,P为等边三角形ABC内一点,PA=3,PB=4,PC=5,求△ABC的面积.