题目内容
8. 如图,已知?ABCD中,AB=6,∠DAB=60°,AC平分∠DAB,E为AB的中点,点F是AC上一动点,求EF+BF的最小值.
如图,已知?ABCD中,AB=6,∠DAB=60°,AC平分∠DAB,E为AB的中点,点F是AC上一动点,求EF+BF的最小值.
分析 根据菱形的对角线互相垂直平分,点B关于AC的对称点是点D,连接ED,EF+BF最小值=ED,然后解直角三角形即可求解.
解答 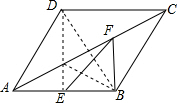 解:在?ABCD中,∵AB∥CD,
解:在?ABCD中,∵AB∥CD,
∴∠ACD=∠CAB,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠DCA,
∴AD=CD,
∴四边形ABCD是菱形,
∴AC与BD互相垂直平分,
∴点B、D关于AC对称,
连接ED,则ED就是所求的EF+BF的最小值的线段,
∵E为AB的中点,∠DAB=60°,
∴DE⊥AB,
∴ED=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴EF+BF的最小值为3$\sqrt{3}$.
点评 本题考查的是轴对称-最短路线问题,涉及到三角形中位线定理和解直角三角形,熟知“两点之间,线段最短”是解答此题的关键.

练习册系列答案
相关题目
3.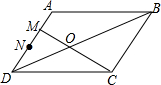 在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
 在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )
在?ABCD中,M,N是AD边上的三等分点,连接BD,MC相交于O点,则$\frac{{S}_{△MOD}}{{S}_{△COB}}$=( )| A. | $\frac{1}{9}$或$\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$或$\frac{2}{3}$ |
17.如果x2+(a+b)•x+5b=x2-x-30,则b为( )
| A. | 5 | B. | -6 | C. | -5 | D. | 6 |

 某市为了迎接新年搞大型庆典活动,在庆典中心竖起(与地面垂直)一个高为4.4米的抛物线形彩虹门(门的厚度不计),如果以过彩门的两个着地点所在直线为x轴,以过门的最高点且垂直地面的直线为y轴建立直角坐标系,则彩虹门可以近似地看成抛物线y=-1.1x2+4.4的一部分,
某市为了迎接新年搞大型庆典活动,在庆典中心竖起(与地面垂直)一个高为4.4米的抛物线形彩虹门(门的厚度不计),如果以过彩门的两个着地点所在直线为x轴,以过门的最高点且垂直地面的直线为y轴建立直角坐标系,则彩虹门可以近似地看成抛物线y=-1.1x2+4.4的一部分,