题目内容
4.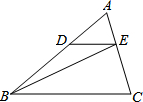 如图,在△ABC中,点D、E分别是AB、AC上的点,DE∥BC,S△ADE:S△BDE=2:3,若S△BEC=15,则S△ABC=( )
如图,在△ABC中,点D、E分别是AB、AC上的点,DE∥BC,S△ADE:S△BDE=2:3,若S△BEC=15,则S△ABC=( )| A. | 14 | B. | 19 | C. | 20 | D. | 25 |
分析 设E到BA的距离是h,根据等底的两个三角形的面积之比等于对应的边之比得出$\frac{AD}{BD}$=$\frac{2}{3}$,根据平行线分线段成比例定理得出$\frac{AE}{EC}$=$\frac{AD}{BD}$=$\frac{2}{3}$,求出$\frac{EC}{AC}$=$\frac{3}{5}$,设B到AC的距离是a,求出$\frac{{S}_{△ABC}}{{S}_{△BEC}}$=$\frac{EC}{AC}$=$\frac{3}{5}$,即可求出答案.
解答 解:设E到BA的距离是h,
∵S△ADE:S△BDE=2:3,
∴($\frac{1}{2}$×AD×h):($\frac{1}{2}$×BD×h)=2:3,
∴$\frac{AD}{BD}$=$\frac{2}{3}$,
∵DE∥BC,
∴$\frac{AE}{EC}$=$\frac{AD}{BD}$=$\frac{2}{3}$,
∴$\frac{EC}{AC}$=$\frac{3}{5}$,
设B到AC的距离是a,
则$\frac{{S}_{△ABC}}{{S}_{△BEC}}$=$\frac{\frac{1}{2}×EC×a}{\frac{1}{2}×AC×a}$=$\frac{EC}{AC}$=$\frac{3}{5}$,
∵S△BEC=15,
∴S△ABC=25,
故选D.
点评 本题考查了三角形的面积公式,平行线分线段成比例定理的应用,能灵活运用等底的两个三角形的面积之比等于对应的边之比是解此题的关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
15.下列不是三棱柱展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
14.一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是( )
| A. | 第一次向右拐40°,第二次向左拐40° | |
| B. | 第一次向右拐50°,第二次向左拐130° | |
| C. | 第一次向右拐50°,第二次向右拐130° | |
| D. | 第一次向左拐50°,第二次向左拐130° |

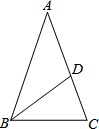 如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一).
如图,在△ABC中,AB=AC,∠A=36°,点D在AC边上,连接BD,若使△ABC与△BDC相似,只需添加一个条件∠ABD=∠A(答案不唯一).