题目内容
2．
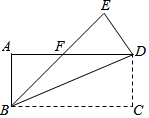如图，把一张长方形纸片ABCD沿对角线BD折叠（长方形的对边平行且相等，每个角都相等），点C落在E处，BE交AD于F．判断三角形BDF的形状，并说明理由．
分析 依据平行线的性质可知∠FDB=∠DBC，然后由翻折的性质可得到∠FBD=∠DBC，故此可证明∠FDB=∠BDF，从而可对三角形的形状作出判断．
解答 解：△BDF为等腰三角形．
理由如下：
由折叠知∠FBD=∠DBC，
∵四边形ABCD为长方形，
∴AD∥BC，
∴∠CBD=∠FDB
∴∠FBD=∠FDB，
∴△BDF为等腰三角形．
点评 本题主要考查的是翻折的性质，矩形的性质、等腰三角形的判定，证得∠FBD=∠FDB是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
8．如图，菱形ABCD放置在直线l上（AB与直线l重合），AB=4，∠DAB=60°，将菱形ABCD沿直线l向右无滑动地在直线l上滚动，从点A离开出发点到点A第一次落在直线l上为止，点A运动经过的路径总长度为（ ）
| A． | $\frac{16\sqrt{3}π}{3}$ | B． | $\frac{16π}{3}$ | C． | $\frac{4π}{3}+\frac{4\sqrt{3}π}{3}$ | D． | $\frac{8π}{3}+\frac{8\sqrt{3}π}{3}$ |
7．
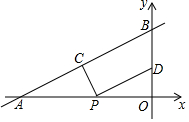如图，在平面直角坐标系中，直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，若点P为OA上一动点，则PC+PD值最小时OP的长为（ ）
如图，在平面直角坐标系中，直线y=$\frac{2}{3}$x+4与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，若点P为OA上一动点，则PC+PD值最小时OP的长为（ ）| A． | 3 | B． | 6 | C． | $\frac{2}{3}$ | D． | $\frac{3}{2}$ |
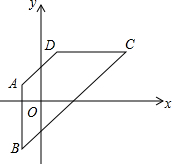如图所示，四边形ABCD的四个顶点A、B、C、D的坐标分别为（-1，1）、（-1，-3）、（5，3）、（1，3），则其对称轴的函数表达式为y=-x+2．
如图，在平面直角坐标系中，半径均为1个单位长度的半圆O1，半圆O2，半圆O3，…，组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒$\frac{π}{2}$个单位长度，则第101秒时，点P的坐标是（101，1）．