题目内容
10. 如图,已知:四边形ABCD中,E为AB的中点,连接CE,DE,CD=CE=BE,DE∥BC.
如图,已知:四边形ABCD中,E为AB的中点,连接CE,DE,CD=CE=BE,DE∥BC.(1)求证:四边形ADCE是菱形;
(2)若BC=6,CE=5,求四边形ADCE的面积.
分析 (1)由△BCE≌△DEC,推出∠BED=∠DCE,推出CD∥BE,由E为AB中点,推出BE=AE,推出CD=AE,推出四边形ADCE是平行四边形,由CD=CE,即可推出四边形ADCE是菱形.
(2)由四边形ADCE是菱形,推出AC⊥DE,由DE∥BC,推出AC⊥BC,推出∠ACB=90°,由E为AB中点,推出CE=$\frac{1}{2}$AB=5,推出AB=10,在Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,根据四边形ADCE的面积=$\frac{1}{2}$•AC•DE即可解决问题.
解答 (1)证明:∵DE∥BC,
∴∠BCE=∠DEC,
∵CD=CE=BE,
∴∠BCE=∠B,∠DEC=∠CDE,
∴∠B=∠CDE,
在△BCE和△DEC中,
$\left\{\begin{array}{l}{∠BCE=∠DEC}\\{∠B=∠CDE}\\{EC=CE}\end{array}\right.$,
∴△BCE≌△DEC,
∴∠BED=∠DCE,
∴CD∥BE,
∵E为AB中点,
∴BE=AE,
∴CD=AE,
∴四边形ADCE是平行四边形,
∵CD=CE,
∴四边形ADCE是菱形,
(2)解:连接AC交DE于点O.
∵△BCE≌△DEC,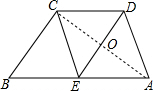
∴DE=BC=6,
∵四边形ADCE是菱形,
∴AC⊥DE,
∵DE∥BC,
∴AC⊥BC,
∴∠ACB=90°,
∵E为AB中点,
∴CE=$\frac{1}{2}$AB=5,
∴AB=10,
在Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8,
∴四边形ADCE的面积=$\frac{1}{2}$•AC•DE=$\frac{1}{2}$×8×6=24.
点评 本题考查平行四边形的判定和性质、菱形的判定和性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案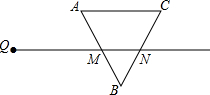 如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从Q出发,沿射线QN以每秒1cm 的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径与△ABC的边相切(切点在边上),则t(单位:秒)可以取的一切值为( )
如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从Q出发,沿射线QN以每秒1cm 的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径与△ABC的边相切(切点在边上),则t(单位:秒)可以取的一切值为( )| A. | t=2 | B. | 3≤t≤7 | C. | t=8 | D. | t=2或3≤t≤7或t=8 |
| A. | x<-1 | B. | x>-1 | C. | x<1 | D. | x>1 |
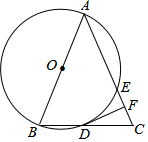 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于F.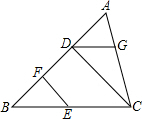 已知:如图,CD⊥AB,EF⊥AB,垂足分别是D,F,∠BEF=∠CDG,试说明:∠B+∠BDG=180°.
已知:如图,CD⊥AB,EF⊥AB,垂足分别是D,F,∠BEF=∠CDG,试说明:∠B+∠BDG=180°.