题目内容
18.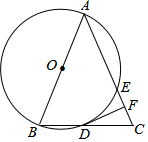 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于F.(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为2,BC=2$\sqrt{2}$,求DF的长.
分析 (1)欲证明DF是⊙O的切线只要证明DF⊥OD,只要证明OD∥AC即可.
(2)连接AD,首先利用勾股定理求出AD,由△ADC∽△DFC可得$\frac{AD}{DF}$=$\frac{AC}{DC}$,列出方程即可解决问题.
解答 (1)证明:连接OD,
∵OB=OD,
∴∠ABC=∠ODB ,
,
∴AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD
∴DF是⊙O的切线
(2)连接AD,
∵AB是⊙O的直径,
∴AD⊥BC,又∵AB=AC
∴BD=DC=$\sqrt{2}$
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{4}^{2}-(\sqrt{2})^{2}}$=,
∵DF⊥AC,
∴△ADC∽△DFC
∴$\frac{AD}{DF}$=$\frac{AC}{DC}$,
∴$\frac{\sqrt{14}}{DF}$=$\frac{4}{\sqrt{2}}$,
∴DF=$\frac{{\sqrt{7}}}{2}$.
点评 本题考查切线的判定、相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.使式子$\frac{\sqrt{x+1}}{x-1}$有意义的x的取值范围是( )
| A. | x>1 | B. | x≠1 | C. | x≥-1且x≠1 | D. | x>-1且x≠1 |
13.若点A(-4,3)、B(m,2)在同一个反比例函数的图象上,则m的值为( )
| A. | 6 | B. | -6 | C. | 12 | D. | -12 |
3.下列关于x的一元二次方程没有实数根的是( )
| A. | x2+2x+4=0 | B. | x2+4x+2=0 | C. | x2+x-1=0 | D. | x2-3x=0 |
 在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: 如图,已知:四边形ABCD中,E为AB的中点,连接CE,DE,CD=CE=BE,DE∥BC.
如图,已知:四边形ABCD中,E为AB的中点,连接CE,DE,CD=CE=BE,DE∥BC.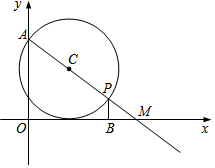 在平面直角坐标系中,A点坐标是(0,6),M点坐标是(8,0).P是射线AM上一点,PB⊥x轴,垂足为B.设AP=A.
在平面直角坐标系中,A点坐标是(0,6),M点坐标是(8,0).P是射线AM上一点,PB⊥x轴,垂足为B.设AP=A.