题目内容
20.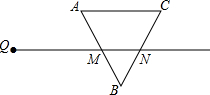 如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从Q出发,沿射线QN以每秒1cm 的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径与△ABC的边相切(切点在边上),则t(单位:秒)可以取的一切值为( )
如图,射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从Q出发,沿射线QN以每秒1cm 的速度向右移动,经过t秒,以点P为圆心,$\sqrt{3}$cm为半径与△ABC的边相切(切点在边上),则t(单位:秒)可以取的一切值为( )| A. | t=2 | B. | 3≤t≤7 | C. | t=8 | D. | t=2或3≤t≤7或t=8 |
分析 根据⊙Q以每秒2cm的速度向左移动,△ABC也沿射线PN以每秒1cm的速度向左移动,确定⊙Q的相对速度,根据已知条件结合图形,求出t可取的一切值.
解答 解:⊙Q以每秒2cm的速度向左移动,△ABC也沿射线PN以每秒1cm的速度向左移动, 相当于△ABC静止,Q以每秒1cm的速度向左移动,
相当于△ABC静止,Q以每秒1cm的速度向左移动,
①当⊙Q与AC相切时,因为半径为$\sqrt{3}$,所以QF=2,
则PQ=2,即t=2,
②作CD⊥PN,BH⊥PN,
∵BE=2,
∴BH=$\sqrt{3}$,HE=1,
同理CD=$\sqrt{3}$,DF=1,
∴当⊙Q在由D到H的过程中与BC相切,此时3≤t≤7,
③当⊙Q与AB相切时,因为半径为$\sqrt{3}$,所以GE=2,即t=8,
综上所述,t=2或3≤t≤7或t=8.
故选:D.
点评 本题考查的是切线的性质,等边三角形的性质,能够分析出所有相切的情形是解题的关键,解答过程中注意圆心到直线距离与圆的半径相等时,直线与圆相切.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
11. 在A、B、C、D四幅图案中,能通过图甲平移得到的是( )
在A、B、C、D四幅图案中,能通过图甲平移得到的是( )
 在A、B、C、D四幅图案中,能通过图甲平移得到的是( )
在A、B、C、D四幅图案中,能通过图甲平移得到的是( )| A. |  | B. |  | C. |  | D. |  |
9.使式子$\frac{\sqrt{x+1}}{x-1}$有意义的x的取值范围是( )
| A. | x>1 | B. | x≠1 | C. | x≥-1且x≠1 | D. | x>-1且x≠1 |
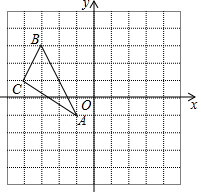 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1),画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标.
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1),画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标. 在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: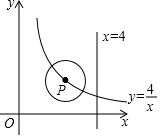 如图,P是双曲线y=$\frac{4}{x}$(x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线x=4相切时,点P的坐标为(3,$\frac{4}{3}$)或(5,$\frac{4}{5}$).
如图,P是双曲线y=$\frac{4}{x}$(x>0)的一个分支上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与直线x=4相切时,点P的坐标为(3,$\frac{4}{3}$)或(5,$\frac{4}{5}$). 如图,是由5个相同的正方体组成的立体图形,从上面观察这个立体图形,得到的平面图形是( )
如图,是由5个相同的正方体组成的立体图形,从上面观察这个立体图形,得到的平面图形是( )



 如图,已知:四边形ABCD中,E为AB的中点,连接CE,DE,CD=CE=BE,DE∥BC.
如图,已知:四边形ABCD中,E为AB的中点,连接CE,DE,CD=CE=BE,DE∥BC.