题目内容
13. 如图,在长方形ABCD中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且△EFG为等腰直角三角形,则EF的长为( )
如图,在长方形ABCD中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且△EFG为等腰直角三角形,则EF的长为( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 12 | D. | 12$\sqrt{2}$ |
分析 首先根据等腰三角形的性质证得△AEG≌△DGF,从而得到AE=DG=6,AG=DF=8,两次利用勾股定理求得结论即可.
解答 解:∵△GEF为等腰直角三角形,
∴GE=GF,∠EGF=90°,
∴∠AGE+DGF=90°,
∵∠AEG+∠AGE=90°,
∴∠AEG=∠DGF,
∴△AEG≌△DGF,
∴AE=GD,AG=DF,
∵AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,
∴AE=DG=6,AG=DF=8,
∴EG=GF=10,
∴EF=$\sqrt{2}$EG=10$\sqrt{2}$,
故选B.
点评 本题考查了矩形的性质及等腰直角三角形的知识,解题的关键是能够利用等腰三角形的性质证得两三角形全等,难度不大.

练习册系列答案
相关题目
3.在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是( )
| A. | 60° | B. | 120° | C. | 60°或 90° | D. | 60°或120° |
1.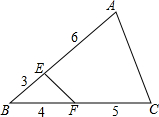 如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )
如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )
 如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )
如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )| A. | 4:23 | B. | 4:25 | C. | 5:26 | D. | 1:6 |
8.已知一元二次方程2x2+px+q=0的两个根是3、-4,则二次三项式2x2+px+q可分解为( )
| A. | (x+3)(x-4) | B. | (x-3)(x+4) | C. | 2(x+3)(x-4) | D. | 2(x-3)(x+4) |
18.$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+$\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为( )
| A. | 1 | B. | $\frac{{2}^{n-2}}{{2}^{n}}$ | C. | 1-$\frac{1}{{2}^{n}}$ | D. | $\frac{{2}^{n}-1}{2n}$ |
5. 如图是用一张长方形纸片折成的,如果∠1=100°,那么∠2的度数是( )
如图是用一张长方形纸片折成的,如果∠1=100°,那么∠2的度数是( )
 如图是用一张长方形纸片折成的,如果∠1=100°,那么∠2的度数是( )
如图是用一张长方形纸片折成的,如果∠1=100°,那么∠2的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
2.x是不大于5的正数,则下列表示正确的是( )
| A. | 0<x<5 | B. | 0<x≤5 | C. | 0≤x≤5 | D. | x≤5 |
 如图,点P在∠AOB内,点M,N分别是点P关于AO,BO的对称点,若△PEF的周长等于20cm,则MN的长为20cm.
如图,点P在∠AOB内,点M,N分别是点P关于AO,BO的对称点,若△PEF的周长等于20cm,则MN的长为20cm.