题目内容
1.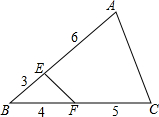 如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )
如图,三角形ABC被分成三角形BEF和四边形AEFC两部分,BE=3,BF=4,FC=5,AE=6,那么三角形BEF面积和四边形AEFC面积的比是( )| A. | 4:23 | B. | 4:25 | C. | 5:26 | D. | 1:6 |
分析 连接AF,根据△BEF的边BE上的高和△ABF边AB上的高相等,推出$\frac{S{\;}_{△BEF}}{S{\;}_{△ABF}}$=$\frac{BE}{AB}=\frac{1}{3}$,推出S△BEF=$\frac{1}{3}$S△ABF,同理得出S△ABF=$\frac{4}{9}$S△ABC,推出S△BEF=$\frac{4}{27}$S△ABC,即可得出答案.
解答 解:连接AF,
∵BE=3,AE=6,
∴AB=9,
∵△BEF的边BE上的高和△ABF边AB上的高相等,
∴$\frac{S{\;}_{△BEF}}{S{\;}_{△ABF}}$=$\frac{BE}{AB}=\frac{1}{3}$,即S△BEF=$\frac{1}{3}$S△ABF,
同理BF=4,CF=5,BC=9,得出S△ABF=$\frac{4}{9}$S△ABC,推出S△BEF=$\frac{4}{27}$S△ABC,
∴S△BEF:S四边形AEFC=4:23,
故选A
点评 本题考查了面积与等积变形的应用,主要考查学生能否灵活运用等高的三角形的面积比等于对应边之比.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
11.若一个两位数的十位上的数字与个位上的数字的和是5,则符合条件的两位数的个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
9. 设▲、
设▲、 、■分别表示三种不同物体.现用天平秤两次,情况如图所示,那么▲、
、■分别表示三种不同物体.现用天平秤两次,情况如图所示,那么▲、 、■这三种物体按质量从大到小排列应为( )
、■这三种物体按质量从大到小排列应为( )
 设▲、
设▲、 、■分别表示三种不同物体.现用天平秤两次,情况如图所示,那么▲、
、■分别表示三种不同物体.现用天平秤两次,情况如图所示,那么▲、 、■这三种物体按质量从大到小排列应为( )
、■这三种物体按质量从大到小排列应为( )| A. | ■、 、▲ 、▲ | B. | ▲、■、 | C. | ■、▲、 | D. |  、▲、■ 、▲、■ |
16. 如图,△ABC中,AB=AC,△DEF是△ABC的内接正三角形,则下列关系式成立的是( )
如图,△ABC中,AB=AC,△DEF是△ABC的内接正三角形,则下列关系式成立的是( )
 如图,△ABC中,AB=AC,△DEF是△ABC的内接正三角形,则下列关系式成立的是( )
如图,△ABC中,AB=AC,△DEF是△ABC的内接正三角形,则下列关系式成立的是( )| A. | 2∠1=∠2+∠3 | B. | 2∠2=∠1+∠3 | C. | 2∠3=∠1+∠2 | D. | ∠1+∠2+∠3=90° |
6.过多边形的一个顶点的所有对角线把多边形分成4个三角形,这个多边形对角线的总条数是( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
13. 如图,在长方形ABCD中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且△EFG为等腰直角三角形,则EF的长为( )
如图,在长方形ABCD中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且△EFG为等腰直角三角形,则EF的长为( )
 如图,在长方形ABCD中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且△EFG为等腰直角三角形,则EF的长为( )
如图,在长方形ABCD中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且△EFG为等腰直角三角形,则EF的长为( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 12 | D. | 12$\sqrt{2}$ |
10.a,b,c不全为0,满足a+b+c=0,a3+b3+c3=0,称使得an+bn+cn=0恒成立的正整数n为“好数”,则不超过2007的正整数中“好数”的个数为( )
| A. | 2 | B. | 1004 | C. | 2006 | D. | 2007 |
11. 如图,在平面直角坐标系中,点P为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
如图,在平面直角坐标系中,点P为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
 如图,在平面直角坐标系中,点P为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )
如图,在平面直角坐标系中,点P为(-2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于( )| A. | -2.5和-3之间 | B. | -3和-3.5之间 | C. | -3.5和-4之间 | D. | -4和-4.5 之间 |