题目内容
2. 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
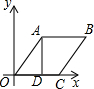
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.(1)如图,平行四边形OABC中,OC在x轴上,将平行四边形OABC沿AD折叠后,点O恰好与点C重合,且∠AOC=60°,AO=4,则点B的坐标为(6,2$\sqrt{3}$).
(2)在一次数学课外实践活动中,小亮的任务是测量学校旗杆的高度,若小亮站在与旗杆底端A在同一水平面上的B处测得旗杆顶端C的仰角为36°,侧倾器的高是1.5m,AB=43m,则旗杆的高度约为32.7m.(用科学计算器计算,使结果精确到0.1)
分析 (1)过点B作BE⊥x轴,垂足为E,连接AC,根据题意可知四边形OABC是菱形、四边形ABED是矩形,即AB=OA=DE=4、BE=AD,在RT△OAD中根据三角函数求得OD=0Acos60°=2、AD=OAsin60°=2$\sqrt{3}$,可得点B坐标;
(2)过点D作DE⊥AC于点E,可得AE=BD=1.5m、DE=AB=43m,在RT△CDE中CE=DEtan∠CDE,根据旗杆高度AC=AE+CE可得.
解答 解:(1)过点B作BE⊥x轴,垂足为E,连接AC,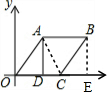
根据折叠可知,OA=AC,OD=CD,
∵∠AOC=60°,
∴△AOC为等边三角形,且AD⊥x轴,
又∵四边形OABC是平行四边形,BE⊥x轴,
∴四边形OABC是菱形,四边形ABED是矩形,
∴AB=OA=DE,BE=AD,
在RT△OAD中,∵OA=4,
∴OD=0Acos60°=4×$\frac{1}{2}$=2,
AD=OAsin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴OE=OD+DE=6,BE=2$\sqrt{3}$,
故点B的坐标为(6,2$\sqrt{3}$);
(2)如图2,过点D作DE⊥AC于点E,则四边形ABED是矩形,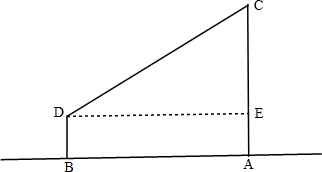
∴AE=BD=1.5m,DE=AB=43m,
在RT△CDE中,∵∠CDE=36°,tan∠CDE=$\frac{CE}{DE}$,
∴CE=DEtan∠CDE=43tan36°,
故旗杆高度AC=AE+CE=1.5+43tan36°≈32.7m.
故答案为:(1)(6,2$\sqrt{3}$);(2)32.7m.
点评 本题考查了解直角三角形的应用,解答本题的关键是熟练掌握锐角三角函数的定义,借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

| A. | $\sqrt{4}$是无理数 | B. | $\sqrt{16}$的平方根是±4 | C. | 0的相反数是0 | D. | -0.5的倒数是2 |
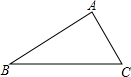 已知:如图△ABC,∠ACB=2∠B=60°,BC=4.请按要求进行尺规作图,作∠ACB的平分线交AB于点D,再过点D作DE⊥BC,垂足为E,并求出AD的长.(不写作法,保留作图痕迹).
已知:如图△ABC,∠ACB=2∠B=60°,BC=4.请按要求进行尺规作图,作∠ACB的平分线交AB于点D,再过点D作DE⊥BC,垂足为E,并求出AD的长.(不写作法,保留作图痕迹).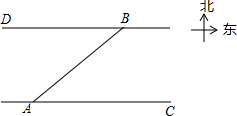 如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?
如图,一艘客轮以30km/h的速度由A码头出发沿北偏东53°方向航行至B码头,已知A、B两码头所在的河岸均为东西走向,河宽为16km,求该客轮至少用多长时间才能到达B码头?
 解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.