题目内容
1.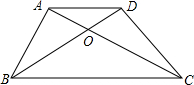 如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.
如图,梯形ABCD中,OD:OB=2:3,三角形AOB的面积是6平方厘米,求梯形ABCD的面积.
分析 先三角形面积公式,利用同底等高得到S△ABC=S△DBC,则S△ABO=S△DOC=6,再利用OD:OB=2:3得到S△AOD=4,然后证明△AOD∽△COB,则根据相似三角形面积的比等于相似比的平方可计算出S△COB,从而可得到梯形的面积.
解答 解:∵AD∥BC,
∴S△ABC=S△DBC,即S△ABO+S△OBC=S△DOC+S△OBC,
∴S△ABO=S△DOC=6,
∵OD:OB=2:3,
∴S△AOD:S△ABO=2:3,
∴S△AOD=4,
∵AD∥BC,
∴△AOD∽△COB,
∴$\frac{{S}_{△AOD}}{{S}_{△COB}}$=($\frac{OD}{OB}$)2=$\frac{4}{9}$,
∴S△COB=9,
∴S梯形ABCD=4+6+9+6=25(平方厘米).
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.解决本题的关键是利用相似三角形面积的比等于相似比的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.有一列数a1,a2,a3,a4,…an,从第二个数开始,每一个数都等于1与它前面那个数的倒数差,如:a1=3,则a2=1-$\frac{1}{3}$=$\frac{2}{3}$,a3=1-$\frac{3}{2}$=-$\frac{1}{2}$…,请你计算当a1=2时,a2015的值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 2015 |
6.如图,若将如图正方形剪成四块,恰好能拼成如图的矩形,则$\frac{a}{b}$等于( )
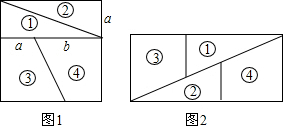

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{5}+1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
11.若x2-5x+6=(x+a)(x+b),a,b的值可能为( )
| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
 解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上.
解不等式组:$\left\{\begin{array}{l}{3(x-2)≤x-4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$并将其解集表示在如图所示的数轴上. 一条笔直的路上A,B,C村庄的位置如图所示,甲从B村出发,向C村方向匀速行驶,经过30分钟,距A村15千米,经过2个小时,距A村30千米,此时乙从B村出发,也向C村方向匀速行驶.
一条笔直的路上A,B,C村庄的位置如图所示,甲从B村出发,向C村方向匀速行驶,经过30分钟,距A村15千米,经过2个小时,距A村30千米,此时乙从B村出发,也向C村方向匀速行驶.