题目内容
12．利用加减消元法解方程组$\left\{\begin{array}{l}{2x+5y=3①}\\{5x-3y=6②}\end{array}\right.$，下列做法正确的是（ ）| A． | 要消去y，可以将①×5+②×2 | B． | 要消去x，可以将①×3+②×（-5） | ||
| C． | 要消去y，可以将①×5+②×3 | D． | 要消去x，可以将①×（-5）+②×2 |
分析 原式利用加减消元法变形得到结果，即可作出判断．
解答 解：利用加减消元法解方程组$\left\{\begin{array}{l}{2x+5y=3①}\\{6x-3y=6②}\end{array}\right.$，
要消去y，可以将①×3+②×5；要消去x，可以将①×（-5）+②×2，
故选D
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
10．以下是某市自来水价格调整表：
自来水价格调整表（部分） 单位：元/立方米
则AC调整水价后某户居民月用水量x（立方米）与应交水费y（元）的函数图象是（ ）
自来水价格调整表（部分） 单位：元/立方米
| 用水类别 | 现行水价 | 拟调整后水价 |
| 一、居民生活用水 | 0.72 | |
| 1．一户一表 | ||
| 第一阶梯：月用水量在 0～30立方米/户 | 0.82 | |
| 第二阶梯：月用水量超过 30立方米/户 | 1.23 | |
| 2．集体表 | 略 |
| A． |  | B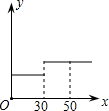． |  | C． |  | D． |  |
7．
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论正确的（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论正确的（ ）| A． | abc＞0 | |
| B． | 9a+3b+c＞0 | |
| C． | a+b≥m（am+b）（m≠1的实数） | |
| D． | 方程ax2+bx+c=2有两个不相等的实数根 |
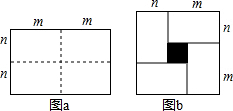
如图，正方形A1A2A3A4，A5A6A7A8，A9A10A11A12，…，（每个正方形从第三象限的顶点开始，按顺时针方向顺序，依次记为A1，A2，A3，A4；A5，A6，A7，A8；A9，A10，A11，A12；…）的中心均在坐标原点O，各边均与x轴或y轴平行，若它们的边长依次是2，4，6…，则顶点A2015的坐标为（504，504）．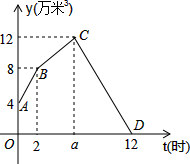
某水电站兴建了一个最大蓄水容量为12万米3的蓄水池，并配有2个流量相同的进水口和1个出水口．某天从0时至12时，进行机组试运行．其中，0时至2时打开2个进水口进水；2时，关闭1个进水口减缓进水速度，至蓄水池中水量达到最大蓄水容量后，随即关闭另一个进水口，并打开出水口，直至12时蓄水池中的水放完为止．若这3个水口的水流都是匀速的，水池中的蓄水量y（万米3）与时间t（时）之间的关系如图所示，请根据图象解决下列问题：