题目内容
4.若抛物线y=ax2+k(a≠0)与y=-2x2+4关于x轴对称,则a=2,k=-4.分析 由y=-2x2+4的顶点坐标为(0,4),对称轴x=0,又因为y=ax2+k(a≠0)与y=-2x2+4关于x轴对称,开口向下,所以抛物线y=ax2+k(a≠0)的顶点坐标为(0,-4),对称轴为x=0,开口向上,所以抛物线的解析式为y=2(x-0)2-4,由此即可解决问题.
解答 解:∵y=-2x2+4的顶点坐标为(0,4),对称轴x=0,
又∵y=ax2+k(a≠0)与y=-2x2+4关于x轴对称,开口向下,
∴抛物线y=ax2+k(a≠0)的顶点坐标为(0,-4),对称轴为x=0,开口向上,
∴抛物线的解析式为y=2(x-0)2-4,
∴a=2,k=-4,
故答案为2,-4.
点评 本题考查二次函数图象与几何变换、轴对称的性质等知识,解题的关键是熟练应用所学知识解决问题,确定抛物线的顶点坐标,开口方向是本题的突破点,所以中考常考题型.

练习册系列答案
相关题目
15.下列各方程的变形,正确的是( )
| A. | 由3+x=5,得x=5+3 | B. | 由7x=$\frac{1}{7}$,得x=49 | C. | 由$\frac{1}{2}$y=0,得y=2 | D. | 由3=x-2,得x=2+3 |
9.去年,中央财政安排资金11200000000元,免除城市义务教育学生学杂费,支持进城务工人员随迁子女接受义务教育,这个数据用科学记数法表示为( )
| A. | 1.1×1011 | B. | 1.12×1010 | C. | 1.12×1011 | D. | 112×108 |
 如图,AE=AD,要使△ABE≌△ACD,应添加的条件是∠C=∠B(答案不唯一)(添加一个条件即可)
如图,AE=AD,要使△ABE≌△ACD,应添加的条件是∠C=∠B(答案不唯一)(添加一个条件即可)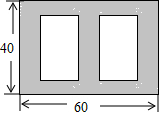 如图,在长60m,宽40m的长方形花园中,欲修宽度相等的观赏路(图中阴影部分),要使观赏路面积占总面积的$\frac{7}{16}$,求观赏路面宽是多少m.
如图,在长60m,宽40m的长方形花园中,欲修宽度相等的观赏路(图中阴影部分),要使观赏路面积占总面积的$\frac{7}{16}$,求观赏路面宽是多少m.