题目内容
16.解方程:(1)3x=10-2x;
(2)3(x-1)=12;
(3)$\frac{x-1}{2}$=$\frac{1}{3}$;
(4)x-$\frac{x-1}{2}$=2-$\frac{x+2}{3}$.
分析 (1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)移项合并得:x=10;
(2)去括号得:3x-3=12,
移项合并得:3x=15,
解得:x=5;
(3)去分母得:3x-3=2,
移项合并得:3x=5,
解得:x=$\frac{5}{3}$;
(4)去分母得:6x-3x+3=12-2x-4,
移项合并得:5x=5,
解得:x=1.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
相关题目
6. 如图所示,△ABC为直角三角形,∠ACB=90°,CD⊥AB,与∠1互余的角有( )
如图所示,△ABC为直角三角形,∠ACB=90°,CD⊥AB,与∠1互余的角有( )
 如图所示,△ABC为直角三角形,∠ACB=90°,CD⊥AB,与∠1互余的角有( )
如图所示,△ABC为直角三角形,∠ACB=90°,CD⊥AB,与∠1互余的角有( )| A. | ∠B | B. | ∠A | C. | ∠BCD和∠A | D. | ∠BCD |
7.下列去括号中,正确的是( )
| A. | a2-(-4a+3)=a2+4a+3 | B. | a2+(-3-4a)=a2-3+4a | ||
| C. | (a-3b)-(4c-2)=a-3b-4c+2 | D. | a-(c-d)=a-c-d |
11.已知关于x的一元一次方程2x-a=0的解是x=1,则a的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
5.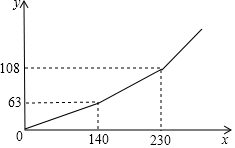 为促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中的折线反映了每户居民每月用电电费y(单位:元)与用电量x(单位:度)间的函数关系.
为促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中的折线反映了每户居民每月用电电费y(单位:元)与用电量x(单位:度)间的函数关系.
(1)根据图象,阶梯电价方案分为三个档次,请填写下表:
(2)小明家某月用电70度,需交电费31.5元;
(3)求第二档每月电费y(元)与用电量x(单位:度)之间的函数表达式;
(4)在每月用电量超过230度时,每度电比第二档多m元,小刚家某月用电290度,缴纳电费153元,求m的值.
 为促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中的折线反映了每户居民每月用电电费y(单位:元)与用电量x(单位:度)间的函数关系.
为促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中的折线反映了每户居民每月用电电费y(单位:元)与用电量x(单位:度)间的函数关系.(1)根据图象,阶梯电价方案分为三个档次,请填写下表:
| 档次 | 第一档 | 第二档 | 第三档 |
| 每月用电量x(度) | 0<x≤140 | 140<x≤230 | x>230 |
(3)求第二档每月电费y(元)与用电量x(单位:度)之间的函数表达式;
(4)在每月用电量超过230度时,每度电比第二档多m元,小刚家某月用电290度,缴纳电费153元,求m的值.
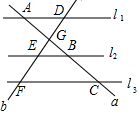 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,直线a、b交于点G,若BC=3BG,AG=2,BG=3,则DE:EF=5:9.
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,直线a、b交于点G,若BC=3BG,AG=2,BG=3,则DE:EF=5:9.