题目内容
14．在△ABC中，∠C=90°，sinA=$\frac{3}{5}$，AB=10，求AC的长．分析 首先由正弦函数的定义可知：$\frac{BC}{AB}$=$\frac{3}{5}$，从而可求得BC的长，然后由勾股定理可求得AC的长
解答 
解：如图所示：
∵sin∠A=$\frac{BC}{AB}$=$\frac{3}{5}$，AB=10，
∴BC=6，
由勾股定理得：AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8．
点评 本题主要考查的是解直角三角形，掌握勾股定理和正弦函数的定义是解题的关键．
练习册系列答案
相关题目
5．
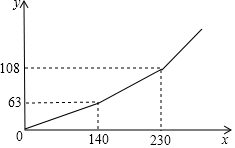为促进节能减排，倡导节约用电，某市将实行居民生活用电阶梯电价方案，图中的折线反映了每户居民每月用电电费y（单位：元）与用电量x（单位：度）间的函数关系．
（1）根据图象，阶梯电价方案分为三个档次，请填写下表：
（2）小明家某月用电70度，需交电费31.5元；
（3）求第二档每月电费y（元）与用电量x（单位：度）之间的函数表达式；
（4）在每月用电量超过230度时，每度电比第二档多m元，小刚家某月用电290度，缴纳电费153元，求m的值．
为促进节能减排，倡导节约用电，某市将实行居民生活用电阶梯电价方案，图中的折线反映了每户居民每月用电电费y（单位：元）与用电量x（单位：度）间的函数关系．（1）根据图象，阶梯电价方案分为三个档次，请填写下表：
| 档次 | 第一档 | 第二档 | 第三档 |
| 每月用电量x（度） | 0＜x≤140 | 140＜x≤230 | x＞230 |
（3）求第二档每月电费y（元）与用电量x（单位：度）之间的函数表达式；
（4）在每月用电量超过230度时，每度电比第二档多m元，小刚家某月用电290度，缴纳电费153元，求m的值．
2．若分式$\frac{a}{a+b}$中的a、b都同时扩大2倍，则该分式的值（ ）
| A． | 不变 | B． | 扩大2倍 | C． | 缩小2倍 | D． | 扩大4倍 |
9．一组数据：2，3，2，6，2，7，6的众数是（ ）
| A． | 2 | B． | 3 | C． | 6 | D． | 7 |
如图，△ABC中AB的垂直平分线交AC于点D，已知∠ABC=∠ACB，AB=9，△BCD的周长等于11，则BC的长是2．