题目内容
17.化简:($\frac{1}{{a}^{2}-ab+{b}^{2}}$-$\frac{b-a}{{a}^{3}-{b}^{3}}$)÷$\frac{{a}^{4}-{a}^{2}{b}^{2}-2{b}^{4}}{({a}^{6}-{b}^{6})-({a}^{4}+{a}^{2}{b}^{2}+{b}^{4})}$.分析 先利用立方差公式把分子分母因式分解,再把括号内通分和把除法运算化为乘法运算,然后约分即可.
解答 解:原式=[$\frac{1}{{a}^{2}-ab+{b}^{2}}$+$\frac{a-b}{(a-b)({a}^{2}+ab+{b}^{2})}$]÷$\frac{({a}^{2}-2{b}^{2})({a}^{2}+{b}^{2})}{({a}^{2}-{b}^{2})({a}^{4}+{a}^{2}{b}^{2}+{b}^{4})-({a}^{4}+{a}^{2}{b}^{2}+{b}^{4})}$
=$\frac{{a}^{2}+ab+{b}^{2}+{a}^{2}-ab+{b}^{2}}{[{(a}^{2}+{b}^{2})-ab][({a}^{2}+{b}^{2})+ab]}$•$\frac{({a}^{4}+{a}^{2}{b}^{2}+{b}^{4})({a}^{2}-{b}^{2}-1)}{({a}^{2}-2{b}^{2})({a}^{2}+{b}^{2})}$
=$\frac{2({a}^{2}+{b}^{2})}{{a}^{4}+{a}^{2}{b}^{2}+{b}^{4}}$•$\frac{({a}^{4}+{a}^{2}{b}^{2}+{b}^{4})({a}^{2}-{b}^{2}-1)}{({a}^{2}-2{b}^{2})({a}^{2}+{b}^{2})}$
=$\frac{2{a}^{2}-2{b}^{2}-2}{{a}^{2}-2{b}^{2}}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.

练习册系列答案
相关题目
8.若线段AB=BC+AC,则关于点C正确的是( )
| A. | C是AB的中点 | |
| B. | C不是AB的中点 | |
| C. | C不是AB的中点,A,B,C不共线 | |
| D. | C不一定是AB的中点,A,B,C三点共线 |
12.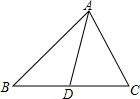 如图,△ACD∽△BCA,则下列各式中一定成立的是( )
如图,△ACD∽△BCA,则下列各式中一定成立的是( )
 如图,△ACD∽△BCA,则下列各式中一定成立的是( )
如图,△ACD∽△BCA,则下列各式中一定成立的是( )| A. | $\frac{AC}{CD}$=$\frac{AB}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=CD•BC |
9.下列说法正确的是( )
| A. | -|-2|=-(-2) | B. | (-1)2n=1(n是正整数) | ||
| C. | -(-a-b)=a-b | D. | 2x3y-3x2y-1是三次三项式 |
6.关于x的方程2x+a-10=0与3x-9=0的解相同,则a的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
7. 有理数a,b在数轴上的位置如图所示,以下说法正确的是( )
有理数a,b在数轴上的位置如图所示,以下说法正确的是( )
 有理数a,b在数轴上的位置如图所示,以下说法正确的是( )
有理数a,b在数轴上的位置如图所示,以下说法正确的是( )| A. | a+b=0 | B. | a-b>0 | C. | ab>0 | D. | |b|<|a| |
 如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;
如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;