题目内容
12.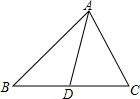 如图,△ACD∽△BCA,则下列各式中一定成立的是( )
如图,△ACD∽△BCA,则下列各式中一定成立的是( )| A. | $\frac{AC}{CD}$=$\frac{AB}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=CD•BC |
分析 根据相似三角形的对应边的比相等列出比例式,对各个选项进行判断即可.
解答 解:∵△ACD∽△BCA,
∴$\frac{AC}{CD}$=$\frac{BC}{AC}$,A不正确;
$\frac{CD}{AD}$=$\frac{AC}{AB}$,B不正确;
$\frac{AC}{CD}$=$\frac{BC}{AC}$,则AC2=CD•BC,C不正确;D正确,
故选:D.
点评 本题考查的是相似三角形的性质,掌握相似三角形的对应角相等,对应边的比相等是解题的关键.

练习册系列答案
相关题目
2.将三个大小不同的正方形如图放置,顶点处两两相接,若正方形A的边长为4,C的边长为3,则B的边长为( )
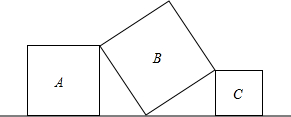

| A. | 25 | B. | 12 | C. | 7 | D. | 5 |
 (1)点C是线段AB上的一点,M、N分别是线段AC、CB的中点.已知AC=4,CB=6.求MN的长.
(1)点C是线段AB上的一点,M、N分别是线段AC、CB的中点.已知AC=4,CB=6.求MN的长.
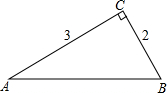 如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA.
如图,在Rt△ABC中,∠C=Rt∠,AC=3,BC=2.求sinA,cosA,tanA. 如图,在△ABC中,D为AC上一点,且CD=CB,CE平分∠ACB,DF∥AB,求证:DB平分∠EDF.
如图,在△ABC中,D为AC上一点,且CD=CB,CE平分∠ACB,DF∥AB,求证:DB平分∠EDF.