题目内容
4.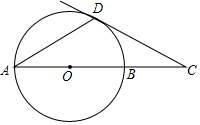 如图1,⊙O的直径AB=2,⊙O的切线CD与AB的延长线交于点C,D为切点,∠C=30°,则AD等于( )
如图1,⊙O的直径AB=2,⊙O的切线CD与AB的延长线交于点C,D为切点,∠C=30°,则AD等于( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 直接利用切线的性质结合锐角三角函数关系进而得出DC的长,即可得出答案.
解答  解:连接OD,
解:连接OD,
∵⊙O的切线CD,D为切点,
∴∠ODC=90°,
∵∠C=30°,⊙O的直径AB=2,
∴CO=2DO=2,∠DOC=60°,
∵AO=DO,
∴∠DAO=∠ODA=30°,
∴∠DAC=∠C=30°,
∴AD=DC=CO•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
故选:C.
点评 此题主要考查了切线的性质以及锐角三角函数关系,正确得出DC的长是解题关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
19.下列各式中,计算正确的是( )
| A. | (15x2y-5xy2)÷5xy=3x-5y | B. | 98×102=(100-2)(100+2)=9996 | ||
| C. | $\frac{x}{x+3}-1=\frac{3}{x+3}$ | D. | (3x+1)(x-2)=3x2+x-2 |
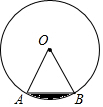 如图,在半径为6的⊙O中,弦AB长为6.求弦AB与$\widehat{AB}$所围成的阴影部分的面积.
如图,在半径为6的⊙O中,弦AB长为6.求弦AB与$\widehat{AB}$所围成的阴影部分的面积. 如图,已知AC=BD,AF∥DE,请你添一个条件,∠ACF=∠DBE,使△AFC≌△DEB.
如图,已知AC=BD,AF∥DE,请你添一个条件,∠ACF=∠DBE,使△AFC≌△DEB.