题目内容
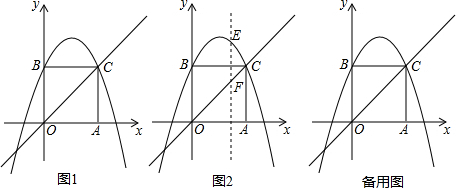
如图所示,动点A、B同时从原点O出发,运动的速度都是每秒1个单位,动点A沿x轴正方向运动,动点B沿y轴正方向运动,以OA、OB为邻边建立正方形OACB,抛物线y=-x2+bx+c经过B、C两点,假设A、B两点运动的时间为t秒:
(1)直接写出直线OC的解析式;
(2)当t=3秒时,求此时抛物线的解析式;此时抛物线上是否存在一点D,使得S△BCD=6?若存在,求出点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,有一条平行于y轴的动直线l,交抛物线于点E,交直线OC于点F,若以O、B、E、F四个点构成的四边形是平行四边形,求点F的坐标;
(4)在动点A、B运动的过程中,若正方形OACB内部有一个点P,且满足OP=
,CP=2,∠OPA=135°,直接写出此时AP的长度.
(1)直接写出直线OC的解析式;
(2)当t=3秒时,求此时抛物线的解析式;此时抛物线上是否存在一点D,使得S△BCD=6?若存在,求出点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,有一条平行于y轴的动直线l,交抛物线于点E,交直线OC于点F,若以O、B、E、F四个点构成的四边形是平行四边形,求点F的坐标;
(4)在动点A、B运动的过程中,若正方形OACB内部有一个点P,且满足OP=
| 2 |

考点:二次函数综合题
专题:压轴题
分析:(1)根据正方形的性质可得∠AOC=45°,然后写出直线OC的解析式即可;
(2)求出OA、OB,然后写出点B、C的坐标,再利用待定系数法求二次函数解析式解答,设BC边上的高为h,利用三角形的面积求出h,从而确定出点P的纵坐标,再代入抛物线解析式求解即可;
(3)分点E在点F上方和下方两种情况表示出EF,再根据平行四边形对边相等列方程求解即可;
(4)将△AOP绕点A逆时针旋转90°得到△AP′C,根据旋转的性质可得AP′=AP,P′C=OP,∠AP′C=∠OPA,然后判断出△APP′是等腰直角三角形,再求出∠PP′C=90°,利用勾股定理列式求出PP′,再根据等腰直角三角形的性质解答.
(2)求出OA、OB,然后写出点B、C的坐标,再利用待定系数法求二次函数解析式解答,设BC边上的高为h,利用三角形的面积求出h,从而确定出点P的纵坐标,再代入抛物线解析式求解即可;
(3)分点E在点F上方和下方两种情况表示出EF,再根据平行四边形对边相等列方程求解即可;
(4)将△AOP绕点A逆时针旋转90°得到△AP′C,根据旋转的性质可得AP′=AP,P′C=OP,∠AP′C=∠OPA,然后判断出△APP′是等腰直角三角形,再求出∠PP′C=90°,利用勾股定理列式求出PP′,再根据等腰直角三角形的性质解答.
解答:解:(1)∵四边形OABC是正方形,
∴∠AOC=45°,
∴直线OC的解析式为y=x;
(2)∵t=3秒,
∴OA=OB=3,
∴点B(0,3),C(3,3),
将点B、C代入抛物线得,
,
解得
,
∴抛物线解析式为y=-x2+3x+3,
设BC边上的高为h,
∵BC=OA=3,S△BCD=6,
∴h=4,
∴点D的纵坐标为3-4=-1,
令y=-1,则-x2+3x+3=-1,
整理得,x2-3x-4=0,
解得x1=-1,x2=4,
所以,D1(-1,-1),D2(4,-1);
(3)∵OB=3,
∴EF=3,
设E(m,-m2+3m+3),F(m,m),
若E在F上方,则,-m2+3m+3-m=3,
整理得,m2-2m=0,
解得m1=0(舍去),m2=2,
∴F1(2,2),
若F在E上方,则,m-(-m2+3m+3)=3,
整理m2-2m-6=0,
解得m1=1-
,m2=1+
,
∴F2(1-
,1-
),
F3(1+
,1+
);
(4)如图,将△AOP绕点A逆时针旋转90°得到△AP′C,
由旋转的性质得,AP′=AP,P′C=OP=
,∠AP′C=∠OPA=135°,
∵△APP′是等腰直角三角形,
∴∠AP′P=45°,
∴∠PP′C=135°-45°=90°,
由勾股定理得,PP′=
=
=
,
所以,AP=
PP′=
×
=1.
∴∠AOC=45°,
∴直线OC的解析式为y=x;
(2)∵t=3秒,
∴OA=OB=3,
∴点B(0,3),C(3,3),
将点B、C代入抛物线得,
|
解得
|
∴抛物线解析式为y=-x2+3x+3,
设BC边上的高为h,
∵BC=OA=3,S△BCD=6,
∴h=4,
∴点D的纵坐标为3-4=-1,
令y=-1,则-x2+3x+3=-1,
整理得,x2-3x-4=0,
解得x1=-1,x2=4,
所以,D1(-1,-1),D2(4,-1);
(3)∵OB=3,
∴EF=3,
设E(m,-m2+3m+3),F(m,m),
若E在F上方,则,-m2+3m+3-m=3,
整理得,m2-2m=0,
解得m1=0(舍去),m2=2,
∴F1(2,2),
若F在E上方,则,m-(-m2+3m+3)=3,
整理m2-2m-6=0,
解得m1=1-
| 7 |
| 7 |
∴F2(1-
| 7 |
| 7 |
F3(1+
| 7 |
| 7 |

(4)如图,将△AOP绕点A逆时针旋转90°得到△AP′C,
由旋转的性质得,AP′=AP,P′C=OP=
| 2 |
∵△APP′是等腰直角三角形,
∴∠AP′P=45°,
∴∠PP′C=135°-45°=90°,
由勾股定理得,PP′=
| PC2-P′C2 |
22-(
|
| 2 |
所以,AP=
| ||
| 2 |
| ||
| 2 |
| 2 |
点评:本题是二次函数综合题型,主要利用了正方形的性质,待定系数法求二次函数解析式,三角形的面积,二次函数图象上点的坐标特征,勾股定理,难点在于(2)求出点D的纵坐标,(3)分情况讨论,(4)利用旋转作出等腰直角三角形和直角三角形.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子
将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,…,依此类推,通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| A、0.5 | B、1 | C、2 | D、4 |
 如图,直线AB、CD相交于点O,则∠AOD的度数是( )
如图,直线AB、CD相交于点O,则∠AOD的度数是( )| A、120° | B、100° |
| C、75° | D、150° |

 如图,是一个长方形鸡场的平面示意图,一边靠墙,另外三面用篱笆围成.若篱笆总长为35m,所围的面积为150m2,求长方形鸡场的长和宽.
如图,是一个长方形鸡场的平面示意图,一边靠墙,另外三面用篱笆围成.若篱笆总长为35m,所围的面积为150m2,求长方形鸡场的长和宽. 如图,如果∠2=100°,那么∠1的同旁内角等于
如图,如果∠2=100°,那么∠1的同旁内角等于