题目内容
解方程
(1)(3x+2)2=25
(2)(2x+1)2=3(2x+1)
(1)(3x+2)2=25
(2)(2x+1)2=3(2x+1)
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法
专题:
分析:(1)首先两边开平方得到3x+2=5或3x+2=-5,然后解一元一次方程即可;
(2)首先提取公因式(2x+1),然后把原方程化为(2x+1)(2x-2)=0,最后解一元一次方程即可.
(2)首先提取公因式(2x+1),然后把原方程化为(2x+1)(2x-2)=0,最后解一元一次方程即可.
解答:解:(1)∵(3x+2)2=25
∴3x+2=5或3x+2=-5,
∴3x=3或3x=-7,
∴x1=1或x2=-
.
(2)∵(2x+1)2=3(2x+1)
∴(2x+1)(2x-2)=0,
∴2x+1=0或2x-2=0,
∴x1=-
,x2=1.
∴3x+2=5或3x+2=-5,
∴3x=3或3x=-7,
∴x1=1或x2=-
| 7 |
| 3 |
(2)∵(2x+1)2=3(2x+1)
∴(2x+1)(2x-2)=0,
∴2x+1=0或2x-2=0,
∴x1=-
| 1 |
| 2 |
点评:本题主要考查了因式分解法和直接开平方法解一元二次方程的知识,解答本题的关键是掌握因式分解法解一元二次方程的步骤,此题难度不大.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下列四种说法中正确的是( )
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;
③锐角和钝角互补; ④若两个角与同一个角互补,则这两个角相等.
①锐角的补角一定是钝角;②一个角的补角一定大于这个角;
③锐角和钝角互补; ④若两个角与同一个角互补,则这两个角相等.
| A、①② | B、①④ |
| C、①②④ | D、①②③④ |
 如图,在△ABC中,AF平分∠BAC,BD⊥AF,BD交AF的延长线于点D,点E在AB上,且ED∥AC,
如图,在△ABC中,AF平分∠BAC,BD⊥AF,BD交AF的延长线于点D,点E在AB上,且ED∥AC,
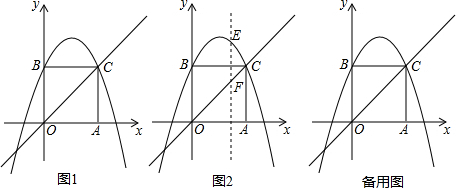
 写出图中所有同位角、内错角、同旁内角.
写出图中所有同位角、内错角、同旁内角.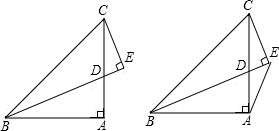 如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.
如图,已知在△ABC中,∠BAC为直角,AB=AC,CE⊥BD于E.