题目内容
9．
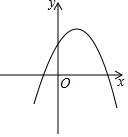二次函数y=ax2-3ax+2（a＜0）的图象如图所示，若y＜2，则x的取值范围为x＜0或x＞3．
分析 函数值y＜2时，函数图象在直线y=2下方，观察图象与直线y=2的交点坐标，可确定x的范围．
解答 解：解ax2-3ax+2=2得，x=0或x=3，
∴抛物线与直线y=2的交点坐标为（0，2），（3，2），
∵开口向下，
∴函数值y＜2的x的取值范围是x＜0或x＞3；
故答案为x＜0或x＞3．
点评 本题考查了二次函数的性质和二次函数的图象，抛物线与直线y=2的交点坐标，开口方向决定了函数值y＜2．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
相关题目
如图，点P的坐标为（1，2）．
如图，在?ABCD中，对角线AC与BD相交于点O，已知∠OAB=90°，OC=3cm，AB=4cm，求BD、AD的长度．
在四边形OABC中，AB∥OC，∠OAB=90°，∠OCB=60°，AB=2，OA=2$\sqrt{3}$．