题目内容
4.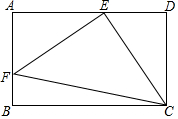 如图,在矩形ABCD中,E为AD上的一点,F为AB上的点,且DE=AF,EF=EC,连结FC.
如图,在矩形ABCD中,E为AD上的一点,F为AB上的点,且DE=AF,EF=EC,连结FC.求证:(1)∠AFE=∠DEC;
(2)△CEF为直角三角形.
分析 (1)由HL证明Rt△AFE≌Rt△DEC,即可得出∠AFE=∠DEC;
(2)由(1)知∠AFE=∠DEC,由∠AFE+∠AEF=90°,得出∠DEC+∠AEF=90°,求出∠CEF=90°即可.
解答 证明:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,
在Rt△AFE和Rt△DEC中,$\left\{\begin{array}{l}{EF=EC}\\{AF=DE}\end{array}\right.$,
∴Rt△AFE≌Rt△DEC(HL),
∴∠AFE=∠DEC;
(2)由(1)知∠AFE=∠DEC,
∵∠AFE+∠AEF=90°,
∴∠DEC+∠AEF=90°,
∴∠CEF=180°-(∠DEC+∠AEF)=90°,
∴△CEF为直角三角形.
点评 本题考查了矩形的性质、全等三角形的判定与性质、直角三角形的性质与判定;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
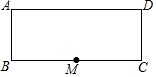 如图是长为20cm,宽为8cm的矩形纸片,M点为长BC边上的中点,沿过M的直线翻折.若顶点B落在对边AD上,那么折痕长度为5$\sqrt{5}$或4$\sqrt{5}$cm.
如图是长为20cm,宽为8cm的矩形纸片,M点为长BC边上的中点,沿过M的直线翻折.若顶点B落在对边AD上,那么折痕长度为5$\sqrt{5}$或4$\sqrt{5}$cm.