题目内容
5.(1)如图1,AB=AD,∠B=∠D,∠1=∠2,求证:△ABC≌△ADE.(2)如图2,已知,AD是△ABC的BC边上的中线,点E,F分别是AD及其延长线上的点,且DE=DF,求证:BF∥CE.

分析 (1)根据ASA即可证明△ABC≌△ADE.
(2)只要证明△CDE≌△BDF,即可推出∠CED=∠F,推出BF∥CE.
解答 证明:(1)∵∠1=∠2,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
$\left\{\begin{array}{l}{∠B=∠D}\\{AB=AD}\\{∠BAC=∠DAE}\end{array}\right.$,
∴△ABC≌△ADE(ASA).
(2)∵AD是△ABC的中线,
∴CD=BD,
在△CDE和△BDF中,
$\left\{\begin{array}{l}{CD=BD}\\{∠CDE=∠BDF}\\{DE=DF}\end{array}\right.$,
∴△CDE≌△BDF,
∴∠CED=∠F,
∴BF∥CE.
点评 本题考查全等三角形的判定和性质、平行线的判定等知识,解题的关键是正确寻找三角形全等的条件,属于基础题,中考常考题型.

练习册系列答案
相关题目
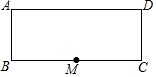 如图是长为20cm,宽为8cm的矩形纸片,M点为长BC边上的中点,沿过M的直线翻折.若顶点B落在对边AD上,那么折痕长度为5$\sqrt{5}$或4$\sqrt{5}$cm.
如图是长为20cm,宽为8cm的矩形纸片,M点为长BC边上的中点,沿过M的直线翻折.若顶点B落在对边AD上,那么折痕长度为5$\sqrt{5}$或4$\sqrt{5}$cm. 如图,点P的坐标为(1,2).
如图,点P的坐标为(1,2). 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离CF为3,则BE=3,阴影部分面积为15.
如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离CF为3,则BE=3,阴影部分面积为15.