题目内容
19．
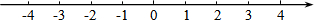解不等式组，并把解集在数轴上表示出来．$\left\{\begin{array}{l}{x-3（x-2）≥4}\\{\frac{5x}{6}+1＞\frac{x-3}{4}}\end{array}\right.$．
分析 分别求出各不等式的解集，再求出其公共解集并在数轴上表示出来即可．
解答 解：$\left\{\begin{array}{l}{x-3（x-2）≥4①}\\{\frac{5x}{6}+1＞\frac{x-3}{4}②}\end{array}\right.$，
解不等式①得，x≤1，
解不等式②得，x＞-3，
故不等式的解集为：-3＜x≤1，
在数轴上表示为：
点评 本题考查的是解一元一次不等式组及在数轴上表示不等式组的解集，熟知实心圆点与空心圆点的区别是解答此题的关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
由几个大小不同的正方形组成的几何图形如图，则它的主视图是（ ）
如图，一次函数y=kx+2的图形与反比例函数y=$\frac{m}{x}$的图象交于点P，点P在第一象限，PA⊥x轴于点A，一次函数的图象分别交x轴、y轴于点C、D，且S△COD=1，$\frac{CO}{OA}=\frac{1}{2}$．
9．在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，CD是AB边上的高，则AD长为（ ）cm．
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{16}{5}$ | D． | $\frac{9}{5}$ |
10．已知方程组$\left\{\begin{array}{l}{a_1}x+y={c_1}\\{a_2}x+y={c_2}\end{array}\right.$的解是$\left\{\begin{array}{l}x=5\\ y=10\end{array}\right.$；则关于x，y的方程组$\left\{\begin{array}{l}{a_1}x-y={a_1}+{c_1}\\{a_2}x-y={a_2}+{c_2}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}x=6\\ y=10\end{array}\right.$ | B． | $\left\{\begin{array}{l}x=6\\ y=-10\end{array}\right.$ | C． | $\left\{\begin{array}{l}x=-6\\ y=10\end{array}\right.$ | D． | $\left\{\begin{array}{l}x=-6\\ y=-10\end{array}\right.$ |