题目内容
9．化简求值（$\frac{2x}{x+2}$-$\frac{x}{x-2}$）÷$\frac{x}{{{x^2}-4}}$，其中x=cos60°tan45°-（-3）分析 先根据分式混合运算的法则把原式进行化简，再求出x的值代入进行计算即可．
解答 解：原式=$\frac{2x（x-2）-x（x+2）}{（x+2）（x-2）}$•$\frac{（x+2）（x-2）}{x}$
=$\frac{2{x}^{2}-4x-{x}^{2}-2x}{（x+2）（x-2）}$•$\frac{（x+2）（x-2）}{x}$
=x-6，
当x=$\frac{1}{2}$×1+3=$\frac{7}{2}$时，原式=x-6=$\frac{7}{2}$-6=-$\frac{5}{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
新思维寒假作业系列答案
相关题目
17．在平面直角坐标系中，点P（1，-1）关于原点的对称点的坐标为（ ）
| A． | （1，1） | B． | （1，-1） | C． | （-1，1） | D． | （-1，-1） |
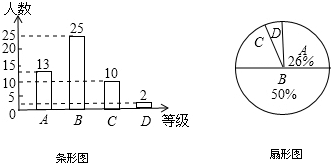
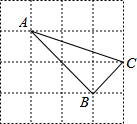如图，由边长为1的小正方形组成的网格中，A、B、C三点都在网格的格点上．则tan∠BAC=$\frac{1}{2}$．
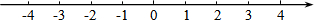解不等式组，并把解集在数轴上表示出来．