��Ŀ����
11�� ��ͼ������ABCD�ı�BC��x���ϣ���A��D�ڵ�һ���ޣ��߶�AB��y����E����EΪAB���е㣬��MΪAC��BD�Ľ��㣬����CE����CE��AB����A������Ϊ��1��2$\sqrt{3}$����
��ͼ������ABCD�ı�BC��x���ϣ���A��D�ڵ�һ���ޣ��߶�AB��y����E����EΪAB���е㣬��MΪAC��BD�Ľ��㣬����CE����CE��AB����A������Ϊ��1��2$\sqrt{3}$������1����ֱ��CE�Ľ���ʽ��
��2����P��ԭ���������x����������ÿ��1����λ�˶����˶�ʱ��Ϊt������P��PQ��BC������EC�ڵ�Q����BCQ���ΪS����S��t֮��Ĺ�ϵʽ��ֱ��д��t��ȡֵ��Χ��
��3��BD���Ƿ���ڵ�F��ʹ��CEFΪֱ�������Σ������ڣ���ֱ��д���߶�MF�ij����������ڣ���˵�����ɣ�
���� ��1�������C��E�������꣬�����ô���ϵ�������ɽ�����⣮
��2����ͼ2�У����������ٵ�0��t��3ʱ��PC=3-t��PQ=$\frac{\sqrt{3}}{3}$��3-t�����ڵ�t��3ʱ��PC=t-3������S=$\frac{1}{2}$•BC•PQ=���ɽ�����⣮
��3�����ڣ���ͼ3�У�������ֱ��BD�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$����F��m��$\frac{\sqrt{3}}{3}$$\frac{3\sqrt{3}+\sqrt{11}}{4}$m+$\frac{\sqrt{3}}{3}$��������F��Rt��CEF��ֱ�Ƕ���ʱ��CE2=CF2+EF2���г����̼��ɽ�����⣬��F��D�غ�ʱ����ECF��ֱ�������Σ���ʱMF1=2$\sqrt{3}$����F��B�غ�ʱ����ECF��ֱ�������Σ���ʱMF2=2$\sqrt{3}$��
��� �⣺��1����ͼ1�У���AK��BC��K��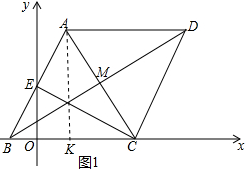
���ı���ABCD�����Σ�
��AB=BC=CD=AD��
��CE��AB��EA=EB��
��CA=CB=AB��
���ABC����ACD�ǵȱ������Σ�
��A��1��2$\sqrt{3}$����
��AK=2$\sqrt{3}$��
��Rt��AKC�У��ߡ�AKC=90�㣬��CAK=30�㣬
��KC=2��AC=AB=BC=4��
��BO=OK=1��OE=$\frac{1}{2}$AK=$\sqrt{3}$��
��E��0��$\sqrt{3}$����C��3��0����
��ֱ��CE�Ľ���ʽΪy=kx+b����$\left\{\begin{array}{l}{b=\sqrt{3}}\\{3k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=\sqrt{3}}\end{array}\right.$��
��ֱ��CE�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$��
��2����ͼ2�У�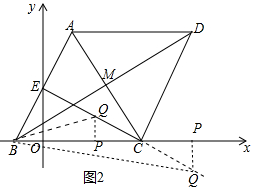
�ٵ�0��t��3ʱ��PC=3-t��PQ=$\frac{\sqrt{3}}{3}$��3-t����
��S=$\frac{1}{2}$•BC•PQ=$\frac{1}{2}$•4•$\frac{\sqrt{3}}{3}$��3-t��=-$\frac{2\sqrt{3}}{3}$t+2$\sqrt{3}$��
�ڵ�t��3ʱ��PC=t-3��
��S=$\frac{1}{2}$•BC•PQ=$\frac{1}{2}$•4•$\frac{\sqrt{3}}{3}$��t-3��=$\frac{2\sqrt{3}}{3}$t-2$\sqrt{3}$��
����������S=$\left\{\begin{array}{l}{-\frac{2\sqrt{3}}{3}t+2\sqrt{3}}&{��0��t��3��}\\{\frac{2\sqrt{3}}{3}t-2\sqrt{3}}&{��t��3��}\end{array}\right.$��
��3�����ڣ��������£���ͼ3�У�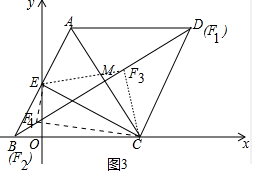
������ֱ��BD�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$����F��m��$\frac{\sqrt{3}}{3}$$\frac{3\sqrt{3}+\sqrt{11}}{4}$m+$\frac{\sqrt{3}}{3}$����
����F��Rt��CEF��ֱ�Ƕ���ʱ��CE2=CF2+EF2��
��32+��$\sqrt{3}$��2=m2+��$\frac{\sqrt{3}}{3}$m+$\frac{\sqrt{3}}{3}$-$\sqrt{3}$��2+��m-3��2+��$\frac{\sqrt{3}}{3}$m+$\frac{\sqrt{3}}{3}$��2��
������2m2-5m-1=0�����m=$\frac{5-\sqrt{33}}{4}$��$\frac{5+\sqrt{33}}{4}$��
��F3��$\frac{5+\sqrt{33}}{4}$��$\frac{3\sqrt{3}+\sqrt{11}}{4}$����F4��$\frac{5-\sqrt{33}}{4}$��$\frac{3\sqrt{3}-\sqrt{11}}{4}$����
��M��2��$\sqrt{3}$����
��F3M=$\frac{\sqrt{11}-\sqrt{3}}{2}$��F4M=$\frac{\sqrt{11}+\sqrt{3}}{2}$��
��F��D�غ�ʱ����ECF��ֱ�������Σ���ʱMF1=2$\sqrt{3}$��
��F��B�غ�ʱ����ECF��ֱ�������Σ���ʱMF2=2$\sqrt{3}$��
��������������CEFΪֱ��������ʱ��MF�ij�Ϊ2$\sqrt{3}$��$\frac{\sqrt{11}-\sqrt{3}}{2}$��$\frac{\sqrt{11}+\sqrt{3}}{2}$��
���� ���⿼��һ�κ����ۺ��⡢����ϵ������ֱ�������ε��ж������ʡ������ε������֪ʶ������Ĺؼ������������Щ֪ʶ��ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮

 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�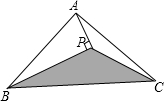 ��ͼ��ʾ��������ABC�����Ϊ1cm2��AP��ֱ��B��ƽ����BP�ڵ�P����������PBC�������$\frac{1}{2}$cm2��
��ͼ��ʾ��������ABC�����Ϊ1cm2��AP��ֱ��B��ƽ����BP�ڵ�P����������PBC�������$\frac{1}{2}$cm2��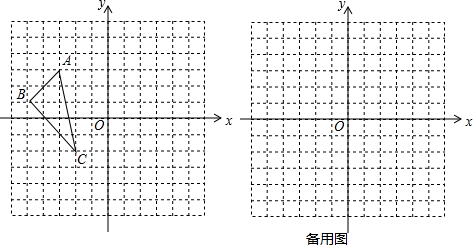
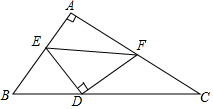 ��ͼ����ABC�У���A=90�㣬AB=3��AC=4����D��BC�ϵĶ��㣬E��F�ֱ���AB��AC�ϣ���EDF=90�㣬����D��E��FΪ��������������ABC���ƣ���BD=$\frac{9}{5}$��$\frac{5}{2}$��
��ͼ����ABC�У���A=90�㣬AB=3��AC=4����D��BC�ϵĶ��㣬E��F�ֱ���AB��AC�ϣ���EDF=90�㣬����D��E��FΪ��������������ABC���ƣ���BD=$\frac{9}{5}$��$\frac{5}{2}$��