题目内容
6.如果矩形的4个顶点分别在原点、反比例函数y=$\frac{k}{x}$图象、x轴和y轴上,那么这个矩形称为反比例函数y=$\frac{k}{x}$图象的伴随矩形.如图(a),矩形AEOF,正方形BGOH都是反比例函数y=$\frac{k}{x}$(k>0,x>0)图象的伴随矩形.(1)当k=6时,①伴随矩形的面积等于6;②在图(b)中用尺规作图的反比例函数y=$\frac{k}{x}$的图象上作出一个点P,使OP=2$\sqrt{3}$;
(2)在图(a)中画直线AB分别交x轴,y轴于点C,D,得图(c),求证:DB:DA=CA:CB;
(3)由DB:DA=CA:CB,你还能得出什么更进一步的结论?请直接写出你的结论.
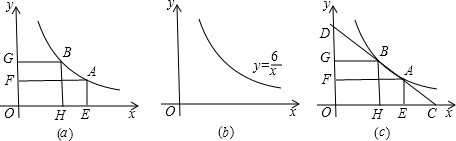
分析 (1)①由矩形的性质和面积得出OE•AE=k=6;②作出第一象限角的平分线,与反比例函数图象的交点即为点P;
(2)由正方形和矩形的性质证明△BDG∽△ADF,△ACE∽△BCH,得出比例式,由伴随矩形的面积相等,即可得出结论;
(3)由(2)容易得出结论:伴随矩形的面积=k(k>0).
解答 (1)解:①∵四边形AEOF是矩形,
∴∠AEO=∠EOF=∠OFA=∠EAF=90°,AE=OF,OE=AF,
∵矩形AEOF的面积=OE•AE,OE•AE=k=6,
∴伴随矩形AEOF的面积=6;
②如图所示: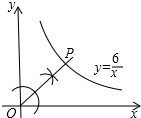
作出第一象限角的平分线,与反比例函数图象的交点即为满足条件的点P;
(2)证明:由(1)①得:正方形BGOH的面积=矩形AEOF的面积=6,
∴BG•BH=AE•AF=6,
∴$\frac{BG}{AF}=\frac{AE}{BH}$,
∵四边形BGOH是正方形,四边形AEOF是矩形,
∴BG=BH,BG∥AF,AE∥BH,
∴△BDG∽△ADF,△ACE∽△BCH,
$\frac{DB}{DA}=\frac{BG}{AF}$,$\frac{CA}{CB}=\frac{AE}{BH}$,
∴$\frac{DB}{DA}=\frac{CA}{CB}$;
(3)解:得出更进一步的结论:伴随矩形的面积=k(k>0);理由如下:
∵DB:DA=CA:CB,
由(2)得:$\frac{DB}{DA}=\frac{BG}{AF}$,$\frac{CA}{CB}=\frac{AE}{BH}$,
∴$\frac{BG}{AF}=\frac{AE}{BH}$,
∴BG•BH=AE•AF=6,
即伴随矩形的面积=k(k>0).
点评 本题是反比例函数综合题目,考查了矩形的性质、矩形面积的计算、尺规作图、相似三角形的判定与性质等知识;本题综合性强,有一定难度,特别是(2)中,需要证明两对三角形相似得出比例式才能得出结论.

| A. | $\frac{9}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{2}{5}$ |
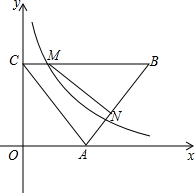 如图,在△ABC中,AB=AC,OA=3,OC=4,BC∥x轴,点M、N分别是线段BC与BA上两点(与线段端点不重合),当△BMN≌△ACO时,反比例函数y=$\frac{k}{x}$的图象经过点M,则k的值是4.
如图,在△ABC中,AB=AC,OA=3,OC=4,BC∥x轴,点M、N分别是线段BC与BA上两点(与线段端点不重合),当△BMN≌△ACO时,反比例函数y=$\frac{k}{x}$的图象经过点M,则k的值是4.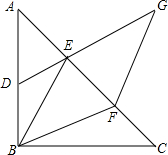 已知∠ABC=90°,AB=BC,F为AC上一点,D,E分别为AB,AF的中点,连接BF,过F作FG∥BE交DE的延长线于G,连接BE,且BE=2DE,AC=6$\sqrt{2}$
已知∠ABC=90°,AB=BC,F为AC上一点,D,E分别为AB,AF的中点,连接BF,过F作FG∥BE交DE的延长线于G,连接BE,且BE=2DE,AC=6$\sqrt{2}$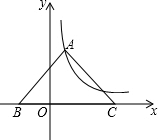 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数y=$\frac{4}{x}$(x>0)的图象上,则OC2-OB2的值为16.
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数y=$\frac{4}{x}$(x>0)的图象上,则OC2-OB2的值为16. 已知在一个5×5的正方形网格中(正方形的边长为1个单位长度)有一个格点△ABC(三角形的各顶点是网格线的交点),且AB=2$\sqrt{5}$,BC=$\sqrt{5}$,AC=5.
已知在一个5×5的正方形网格中(正方形的边长为1个单位长度)有一个格点△ABC(三角形的各顶点是网格线的交点),且AB=2$\sqrt{5}$,BC=$\sqrt{5}$,AC=5.