题目内容
19.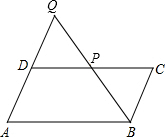 如图,点P在平行四边形ABCD的CD边上,连结BP并延长与AD的延长线交于点Q.
如图,点P在平行四边形ABCD的CD边上,连结BP并延长与AD的延长线交于点Q.(1)求证:△AQB∽△CBP;
(2)当AB=2PC时,求证:点D为AQ的中点.
分析 (1)由AQ∥BC,PD∥AB,从而可得到△DQP∽△CBP,△DQP∽△QAB,从而可证明△AQB∽△CBP;
(2)由△DQP∽△QAB可知:$\frac{DP}{AB}=\frac{QD}{QA}$,然后根据AB=2PC可知$\frac{PD}{AB}=\frac{1}{2}$,从而可证得点D为AQ的中点.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AQ∥BC
∴△DQP∽△CBP
∵PD∥AB,
∴△DQP∽△QAB.
∴△AQB∽△CBP.
(2)∵AB=2PC,
∴DP=CP=$\frac{1}{2}$CD.
∴$\frac{PD}{AB}=\frac{1}{2}$.
∵△DQP∽△QAB,
∴$\frac{QD}{AQ}=\frac{PD}{AB}=\frac{1}{2}$.
∴点D为AQ的中点.
点评 本题主要考查的是相似三角形的性质和判定、平行四边形的性质,证得△DQP∽△CBP、△DQP∽△QAB是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
9.一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)【方差公式:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]】
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分越高成绩越好,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.请问A同学的数学成绩好还是英语成绩好?
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 | $\sqrt{2}$ | |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分越高成绩越好,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.请问A同学的数学成绩好还是英语成绩好?
7.将△ABC三个顶点横坐标都乘以-1,纵坐标不变,则所得图形与原图形的关系是( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 不存在对称关系 |
14.我们学习解二元一次方程组时,通过代入消元法或者加减消元法变二元方程为一元方程,这种解题方法主要体现的数学思想是( )
| A. | 分类讨论 | B. | 化归与转化 | C. | 函数与方程 | D. | 数形结合 |
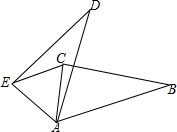 在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得DE∥AB,则∠DAB等于30°.
在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得DE∥AB,则∠DAB等于30°.