题目内容
8.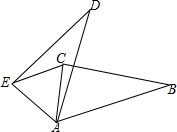 在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得DE∥AB,则∠DAB等于30°.
在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A逆时针旋转到△AED的位置,使得DE∥AB,则∠DAB等于30°.
分析 先利用平行线的性质得∠ACE=∠CAB=75°,再根据旋转的性质得AC=AE,∠DAB=∠EAC,则∠AEC=∠ACE=75°,接着利用三角形内角和定理可计算出∠CAE=30°,于是得到∠DAB=30°.
解答 解:∵CE∥AB,
∴∠ACE=∠CAB=75°,
∵△ABC绕点A逆时针旋转到△AED的位置,
∴AC=AE,∠DAB=∠EAC
∴∠AEC=∠ACE=75°,
∴∠CAE=30°,
∴∠DAB=30°.
故答案为30°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.有一个三角形的两边长分别为4和7,第三边的长是方程(x-5)(x-12)=0的根,则这个三角形的周长为( )
| A. | 16 | B. | 23 | C. | 24 | D. | 16或23 |
3.已知点(a,8)在抛物线y=ax2上,则a的值为( )
| A. | ±2 | B. | ±2$\sqrt{2}$ | C. | 2 | D. | -2 |
13. 如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
 如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HNMO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )| A. | a>b>c | B. | a=b=c | C. | c>a>b | D. | b>c>a |
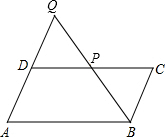 如图,点P在平行四边形ABCD的CD边上,连结BP并延长与AD的延长线交于点Q.
如图,点P在平行四边形ABCD的CD边上,连结BP并延长与AD的延长线交于点Q.
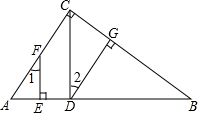 已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.