题目内容
11.羽毛球的标准重量为5g,在检测其重量是否标准时,把超过标准重量的部分用正数,低于标准重量的部分用负数表示.下面是五个羽毛球的重量检测记录(单位:g):+0.25,+0.17,-0.30,+0.03,-0.25.(1)其中最标准和最不标准的羽毛球各重多少g?
(2)这5个羽毛球共重多少克?
(3)平均每个羽毛球重多少克?
分析 (1)根据绝对值最小的是最标准的,绝对值最大的是最不标准的,可得最标准和最不标准的球重;
(2)根据有理数的加法运算,可得球的总重量;
(3)根据球的总重量除以球的个数,可得平均重量.
解答 解:(1)∵|+0.25|=0.25,|+0.17|=0.17;|-0.30|=0.30;|+0.03|=0.03;|-0.25|=0.25.
∵0.30>0.25>0.17>0.03,
最标准的球重:5+0.03=5.03(g)
最不标准的求重:5-0.30=4.70(g).
答:其中最标准的羽毛球重5.03g,最不标准的羽毛球重4.70g;
(2)这5个羽毛球共重:(0.25+0.17-0.30+0.03-0.25)+5×5=24.9(g);
(3)平均每个羽毛球重:24.9÷5=4.98(g).
答:这5个羽毛球共重24.9g,平均每个羽毛球重4.98g.
点评 本题考查了正数和负数,正数和负数绝对值最小的最标准,绝对值最大的最不标准,有理数加法运算是解总重量的关键.

练习册系列答案
相关题目
2.式子$\sqrt{x-1}$在实数范围内有意义,则x的取值范围是( )
| A. | x<1 | B. | x≥1 | C. | x≤-1 | D. | x<-1 |
3.已知点(a,8)在抛物线y=ax2上,则a的值为( )
| A. | ±2 | B. | ±2$\sqrt{2}$ | C. | 2 | D. | -2 |
1. 一条排水管的截面如图所示.已知排水管的水深CD=4,水面宽AB=16,则截面圆半径OB是( )
一条排水管的截面如图所示.已知排水管的水深CD=4,水面宽AB=16,则截面圆半径OB是( )
 一条排水管的截面如图所示.已知排水管的水深CD=4,水面宽AB=16,则截面圆半径OB是( )
一条排水管的截面如图所示.已知排水管的水深CD=4,水面宽AB=16,则截面圆半径OB是( )| A. | 8 | B. | 10 | C. | 12 | D. | $8\sqrt{3}$ |
 读如图提供的信息,回答下列问题.
读如图提供的信息,回答下列问题.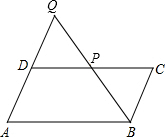 如图,点P在平行四边形ABCD的CD边上,连结BP并延长与AD的延长线交于点Q.
如图,点P在平行四边形ABCD的CD边上,连结BP并延长与AD的延长线交于点Q.