题目内容
(c-a2b2)2 等于（ ）
A. c -ab2 B. c2 -2a2b2c+a4b4 C. c-a2b2c+a4b4 D. c2 -2abc+a4b
B
【解析】根据完全平方公式可得：(c-a2b2)2=c2 -2a2b2c+a4b4 ，故选B.
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．
求证：AF平分∠BAC．
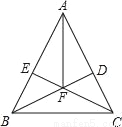
证明见解析.
【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC．
试题解析：证明：∵AB=AC(已知)，
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高，
∴... 如图，MP⊥NP，MQ为△MNP的角平分线，MT＝MP，连接TQ，则下列结论中不正确的是（ ）
A. TQ＝PQ B. ∠MQT＝∠MQP C. ∠QTN＝90° D. ∠NQT＝∠MQT
D
【解析】∵MQ为△MNP的角平分线，
∴∠PMQ=∠QMT，
∵在△PMQ和△TMQ中，
,
∴△PMQ≌△TMQ，
∴TQ=PQ，∠P=∠QTM=90°，∠MQT＝∠MQP，
故A、B、C选项正确，D选项错误.
故选D. （a-b）2 -3（a2+b2）
-2a2-2ab-2b2
【解析】试题分析：先根据完全平方公式计算，再合并同类项即可.
试题解析：
（a-b）2 -3（a2+b2）=a2-2ab+b2-3a2-3b2=-2a2-2ab-2b2. （5-x2）2等于_______；
25-10x2+x4
【解析】根据完全平方公式可得：（5-x2）2=25-10x2+x4. 下面计算正确的是（ ）
A. (a+b)(a-b)=2a+2b B. b5 + b5 = b10 C. x5 .x5 = x25 D. (y-z)2=y2-2yz+z2
D
【解析】选项A，原式=a2-b2 ；选项 B，原式=2b5；选项C，原式=x10 ;选项D，原式= y2-2yz+z2.故选D. 2（a-b）（a+b）-a2+b2
a2-b2
【解析】试题分析：先根据平方差公式计算，再合并同类项即可.
试题解析：
2（a-b）（a+b）-a2+b2=2a2-2b2-a2+b2=a2-b2. 下面计算错误的是（ ）
A. (y-z)(y+z)=y2-z2 B. (m-n)(m+n)=n2-m C. x5·x20 = x25 D. y3 · y5 = y8
B
【解析】根据平方差公式可得：选项A，(y-z)(y+z)=y2-z2；选项B， (m-n)(m+n)=m2-n2；根据同底数幂的乘法法则可得：选项C，x5·x20 = x25；选项D， y3 · y5 = y8.故选B. 若分式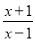
有意义，则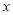
的取值范围是_____．
【解析】根据分式的分母不等于0时，分式有意义，列出不等式即可得出答案.
【解析】
因为分式有意义，
所以，
解得，
故答案为： .