题目内容
1.如图1,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形ABCD,且∠ABC=60°,其他条件不变,如图2.连接DE,试探究线段BP与线段DE的数量关系,并说明理由.

分析 (1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCP=∠DCP,然后利用“边角边”证明即可;
(2)根据全等三角形对应角相等可得∠CBP=∠CDP,根据等边对等角可得∠CBP=∠E,然后求出∠DPE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得证;
(3)结论:DE=PB.只要证明△PDE是等边三角形即可解决问题;
解答 (1)证明:在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,
∵在△BCP和△DCP中,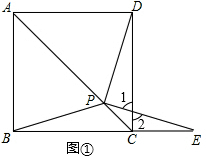
$\left\{\begin{array}{l}{BC=DC}\\{∠BCP=∠DCP}\\{PC=PC}\end{array}\right.$,
∴△BCP≌△DCP(SAS);
(2)证明:由(1)知,△BCP≌△DCP,
∴∠CBP=∠CDP,
∵PE=PB,
∴∠CBP=∠E,
∵∠1=∠2(对顶角相等),
∴180°-∠1-∠CDP=180°-∠2-∠E,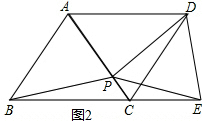
即∠DPE=∠DCE
∵AB∥CD,
∴∠DCE=∠ABC,
∴∠DPE=∠ABC;
(3)解:结论:DE=PB.
理由:由(1)知PD=PB=PE,
由(2)知,∠DPE=∠ABC=60°,
∴△PDE是等边三角形,
∴DE=PE=PB
∴DE=PB.
点评 本题考查了正方形的性质,全等三角形的判定与性质,菱形的性质,等边对等角的性质,熟记正方形的性质确定出∠BCP=∠DCP是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD的面积之比是( )
| A. | 4:3 | B. | 3:4 | C. | 16:9 | D. | 9:16 |
13.费尔兹奖是国际上享有崇高荣誉的一个数学奖项,在国际数学家大会上颁给有卓越贡献的年龄不超过四十岁的年轻数学家,美籍华人丘成桐1982年获费尔兹奖,下面的数据是截至2014年56名费尔兹奖得主获奖时的年龄:
29 39 35 33 39 28 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 29
32 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
根据以上信息将下面的频数分布表补充完整:
29 39 35 33 39 28 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 29
32 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
根据以上信息将下面的频数分布表补充完整:
| 分组 | 划记 | 频数 |
| 25≤x<30 |  | 4 |
| 30≤x<35 | 正正正 | 15 |
| 35≤x<40 | 正正正正正正一 | 31 |
| 40≤x<45 | 正一 | 6 |
10. 实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
 实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )| A. | a>-2 | B. | a<-3 | C. | -a<b | D. | a<-b |
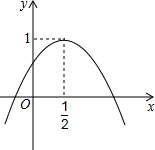 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc>0;②a=b;③a=4c-4;④方程ax2+bx+c=1有两个相等的实数根,其中正确的结论是③④.(只填序号即可).
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc>0;②a=b;③a=4c-4;④方程ax2+bx+c=1有两个相等的实数根,其中正确的结论是③④.(只填序号即可).