��Ŀ����
4��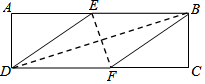 �ھ���ABCD�У���һ������BFDE����E��F�ֱ����߶�AB��CD�ϣ��������ǵ�����ֱ�ΪS����ABCD��S����BEDF����SABCD��SBFDE���������½��ۣ�����$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$����tan��EDF=$\frac{\sqrt{3}}{3}$��
�ھ���ABCD�У���һ������BFDE����E��F�ֱ����߶�AB��CD�ϣ��������ǵ�����ֱ�ΪS����ABCD��S����BEDF����SABCD��SBFDE���������½��ۣ�����$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$����tan��EDF=$\frac{\sqrt{3}}{3}$������DE2=BD•EF����DF=2AD��������
| A�� | ���Ǽ����⣬���Ǽ����� | B�� | ���������⣬���������� | ||
| C�� | ���Ǽ����⣬���������� | D�� | ���������⣬���Ǽ����� |
���� ������֪�����cos��BFC=$\frac{\sqrt{3}}{2}$�������tan��EDF�������жϣ�
����S��DEF=$\frac{1}{2}$DF•AD=$\frac{1}{4}$BD•EF����DE2=BD•EF���ɵ�DF•AD=$\frac{1}{2}$DF2����DF=2AD��
��� �⣺����CF=x��DF=y��BC=h��
���ı���BFDE�����Σ�
��BF=DF=y��DE��BF��
��$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$��
��$\frac{��x+y��h}{yh}$=$\frac{2+\sqrt{3}}{2}$��
��$\frac{x}{y}$=$\frac{\sqrt{3}}{2}$����cos��BFC=$\frac{\sqrt{3}}{2}$��
���BFC=30�㣬
��DE��BF��
���EDF=��BFC=30�㣬
��tan��EDF=$\frac{\sqrt{3}}{3}$��
���Ԣ��������⣮
�ڡ��ı���BFDE�����Σ�
��DF=DE��
��S��DEF=$\frac{1}{2}$DF•AD=$\frac{1}{4}$BD•EF��
�֡�DE2=BD•EF����֪����
��S��DEF=$\frac{1}{4}$DE2=$\frac{1}{4}$DF2��
��DF•AD=$\frac{1}{2}$DF2��
��DF=2AD��
���Ԣ��������⣮
��ѡ��B��
���� ���⿼���˾��ε����ʼ����ε����ʣ�����Ĺؼ��Ǣ��������EDF�����Һ���ֵȷ�������������������У����������ȷ����

| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� | 4��3 | B�� | 3��4 | C�� | 16��9 | D�� | 9��16 |
29�� 39�� 35�� 33�� 39�� 28�� 33�� 35�� 31�� 31�� 37�� 32�� 38�� 36
31�� 39�� 32�� 38�� 37�� 34�� 29�� 34�� 38�� 32�� 35�� 36�� 33�� 29
32�� 35�� 36�� 37�� 39�� 38�� 40�� 38�� 37�� 39�� 38�� 34�� 33�� 40
36�� 36 ��37�� 40�� 31�� 38�� 38�� 40�� 40�� 37�� 35�� 40�� 39�� 37
����������Ϣ�������Ƶ���ֲ�������������
| ���� | ���� | Ƶ�� |
| 25��x��30 |  | 4 |
| 30��x��35 | ������ | 15 |
| 35��x��40 | ������������һ | 31 |
| 40��x��45 | ��һ | 6 |
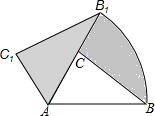 ��ͼ���ڡ�ABC�У���BAC=50�㣬AC=2��AB=3���ֽ���ABC��A����ʱ��ת50��õ���AB1C1����ͼ�е���Ӱ���ֵ����Ϊ$\frac{5}{4}$�У�
��ͼ���ڡ�ABC�У���BAC=50�㣬AC=2��AB=3���ֽ���ABC��A����ʱ��ת50��õ���AB1C1����ͼ�е���Ӱ���ֵ����Ϊ$\frac{5}{4}$�У�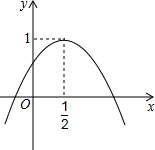 ��ͼ�����κ���y=ax2+bx+c��ͼ����y���������ཻ���䶥������Ϊ��$\frac{1}{2}$��1�������н��ۣ���abc��0����a=b����a=4c-4���ܷ���ax2+bx+c=1��������ȵ�ʵ������������ȷ�Ľ����Ǣۢܣ���ֻ����ż��ɣ���
��ͼ�����κ���y=ax2+bx+c��ͼ����y���������ཻ���䶥������Ϊ��$\frac{1}{2}$��1�������н��ۣ���abc��0����a=b����a=4c-4���ܷ���ax2+bx+c=1��������ȵ�ʵ������������ȷ�Ľ����Ǣۢܣ���ֻ����ż��ɣ���