题目内容
5.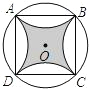 如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π.
如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π.
分析 阴影部分的面积等于正方形ABCD的面积减去四个弓形的面积,而四个弓形的面积为圆的面积减去正方形的面积.
解答 解:由圆内接正方形的性质知,正方形的边长等于半径的$\sqrt{2}$倍,
∴阴影部分的面积=($\sqrt{2}$)2-[4π-($\sqrt{2}$)2]=4-4π.
故答案为:4-4π.
点评 本题考查了圆内接正方形的性质,正确的应用圆的面积公式,正方形的面积公式求解是解题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
13.费尔兹奖是国际上享有崇高荣誉的一个数学奖项,在国际数学家大会上颁给有卓越贡献的年龄不超过四十岁的年轻数学家,美籍华人丘成桐1982年获费尔兹奖,下面的数据是截至2014年56名费尔兹奖得主获奖时的年龄:
29 39 35 33 39 28 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 29
32 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
根据以上信息将下面的频数分布表补充完整:
29 39 35 33 39 28 33 35 31 31 37 32 38 36
31 39 32 38 37 34 29 34 38 32 35 36 33 29
32 35 36 37 39 38 40 38 37 39 38 34 33 40
36 36 37 40 31 38 38 40 40 37 35 40 39 37
根据以上信息将下面的频数分布表补充完整:
| 分组 | 划记 | 频数 |
| 25≤x<30 |  | 4 |
| 30≤x<35 | 正正正 | 15 |
| 35≤x<40 | 正正正正正正一 | 31 |
| 40≤x<45 | 正一 | 6 |
10. 实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
 实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )
实数a,b在数轴上的对应点的位置如图所示,则结论正确的是( )| A. | a>-2 | B. | a<-3 | C. | -a<b | D. | a<-b |
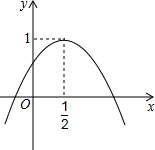 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc>0;②a=b;③a=4c-4;④方程ax2+bx+c=1有两个相等的实数根,其中正确的结论是③④.(只填序号即可).
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc>0;②a=b;③a=4c-4;④方程ax2+bx+c=1有两个相等的实数根,其中正确的结论是③④.(只填序号即可).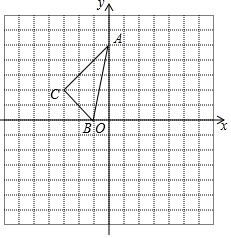 在正方形网格中,每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
在正方形网格中,每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.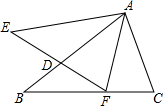 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论: