题目内容
14.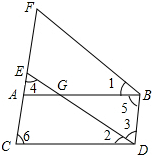 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.证明:∵∠3=∠4(已知)
∴CF∥BD内错角相等,两直线平行
∴∠5+∠CAB=180°(两直线平行,同旁内角互补 )
∵∠5=∠6(已知)
∴∠6+∠CAB=180°(等式的性质)
∴AB∥CD同旁内角互补,两直线平行
∴∠2=∠EGA两直线平行,同位角相等
∵∠1=∠2(已知)
∴∠1=∠EGA等量代换
∴ED∥FB(同位角相等,两直线平行)
分析 由∠3=∠4,根据平行线的判定得出CF∥BD,根据平行线的性质得出∠5+∠CAB=180°,求出∠1=∠EGA,根据平行线的判定得出ED∥FB即可.
解答 证明:∵∠3=∠4(已知),
∴CF∥BD(内错角相等,两直线平行),
∴∠5+∠CAB=180°(两直线平行,同旁内角互补 ),
∵∠5=∠6(已知),
∴∠6+∠CAB=180°(等式的性质),
∴AB∥CD (同旁内角互补,两直线平行),
∴∠2=∠EGA(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠1=∠EGA(等量代换),
∴ED∥FB(同位角相等,两直线平行);
故答案为:内错角相等,两直线平行;两直线平行,同旁内角互补;同旁内角互补,两直线平行;两直线平行,同位角相等;等量代换;同位角相等,两直线平行.
点评 本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质定理是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
14.计算:($\frac{4}{5}$)2014×($\frac{5}{4}$)2015的结果是( )
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | ($\frac{4}{5}$)4029 | D. | ($\frac{5}{4}$)2029 |
9.以$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$为解建立一个二元一次方程,其中不正确的是( )
| A. | 3x-4 y=5 | B. | $\frac{1}{3}$x-y=0 | C. | x+2y=-3 | D. | $\frac{x}{2}$-$\frac{y}{3}$=$\frac{7}{6}$ |
4.小强同学投掷30次实心球的成绩如表所示:
由上表可知小强同学投掷30次实心球成绩的众数与中位数分别是( )
| 成绩(m) | 11.8 | 11.9 | 12 | 12.1 | 12.2 |
| 频数 | 1 | 6 | 9 | 10 | 4 |
| A. | 12m,11.9m | B. | 12m,12.1m | C. | 12.1m,11.9m | D. | 12.1m,12m |
