题目内容
2.约分:(1)$\frac{{-25{a^2}b{c^3}}}{{15a{b^2}c}}$;
(2)$\frac{{{a^2}-4}}{ab+2b}$.
分析 (1)、(2)根据约分的步骤找出分子与分母的公分母,再约去即可.
解答 解:(1)$\frac{{-25{a^2}b{c^3}}}{{15a{b^2}c}}$=$\frac{5abc•(-5)a{c}^{2}}{5abc•3b}$=$-\frac{{5a{c^2}}}{3b}$;
(2)$\frac{{{a^2}-4}}{ab+2b}$=$\frac{(a+2)(a-2)}{b(a+2)}$=$\frac{a-2}{b}$.
点评 本题考查了约分,用到的知识点是分式的基本性质,约去分式的分子与分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分.确定公因式要分为系数、字母、字母的指数来分别确定.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
2.以长度分别为下列各组数的线段为边,其中能构成直角三角形的是( )
| A. | 4,5,6 | B. | 1,1,2 | C. | 6,8,10 | D. | 5,12,14 |
3. 如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
 如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )| A. | ∠DOG与∠BOE互补 | B. | ∠AOE-∠DOF=45° | C. | ∠EOD与∠COG互补 | D. | ∠AOE与∠DOF互余 |
 如图所示,一个点从数轴上的原点开始,先向右移动3单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照下图并思考,完成下列各题.
如图所示,一个点从数轴上的原点开始,先向右移动3单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照下图并思考,完成下列各题.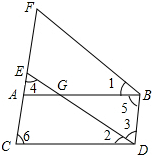 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据. 如图,在等腰Rt△ABC中,∠B=90°,BC=BA=6,D为AC上任意一点,把△CDB绕B点逆时针旋转90°,补充完旋转后的图形,并求出把△CDB旋转后所得的三角形与△ABD的面积之和.
如图,在等腰Rt△ABC中,∠B=90°,BC=BA=6,D为AC上任意一点,把△CDB绕B点逆时针旋转90°,补充完旋转后的图形,并求出把△CDB旋转后所得的三角形与△ABD的面积之和.