题目内容
3.方程组$\left\{\begin{array}{l}{|x|+y=10}\\{x+|y|=4}\end{array}\right.$的解有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 由于x、y的符号不确定,因此本题要分情况讨论.
解答 解:当x≥0,y≤0时,原方程组可化为:$\left\{\begin{array}{l}{x+y=10}\\{x-y=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=7}\\{y=3}\end{array}\right.$;由于y≤0,所以此种情况不成立.
当x≤0,y≥0时,原方程组可化为:$\left\{\begin{array}{l}{-x+y=10}\\{x+y=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-3}\\{y=7}\end{array}\right.$.
当x≥0,y≥0时,$\left\{\begin{array}{l}{x+y=10}\\{x+y=4}\end{array}\right.$,无解;
当x≤0,y≤0时,$\left\{\begin{array}{l}{-x+y=10}\\{x-y=4}\end{array}\right.$,无解;
因此原方程组的解为:$\left\{\begin{array}{l}{x=-3}\\{y=7}\end{array}\right.$.
故选:A.
点评 本题考查了解方程组,在解含有绝对值的二元一次方程组时,要分类讨论,不可漏解.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
3. 如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
 如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )
如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论错误的是( )| A. | ∠DOG与∠BOE互补 | B. | ∠AOE-∠DOF=45° | C. | ∠EOD与∠COG互补 | D. | ∠AOE与∠DOF互余 |
8.某地区为了加大“退耕还林”的力度,出台了一系列的激励措施:在“退耕还林”过程中,每一年的林地面积达到10亩且每年的林地面积在增加的农户,当年都可得生活补贴费2000元,且每超过10亩的部分还给予奖励每亩a元,在林间还有套种其他农作物,平均每亩还有b元的收入.
下表是某农户在头两年通过“退耕还林”每年获得的总收入情况:
(注:年总收入=生活补贴量+政府奖励量+种农作物收入)
(1)试根据以上提供的资料确定a、b的值.
(2)从2015年起,如果该农户每年新增林地的亩数比前一年按相同的增长率增长,那么2017年该农户获得的总收入达到多少元?
下表是某农户在头两年通过“退耕还林”每年获得的总收入情况:
| 年份 | 拥有林地的亩数 | 年总收入 |
| 2014 | 20 | 3100元 |
| 2015 | 26 | 5560元 |
(1)试根据以上提供的资料确定a、b的值.
(2)从2015年起,如果该农户每年新增林地的亩数比前一年按相同的增长率增长,那么2017年该农户获得的总收入达到多少元?
13.1000万用科学记数法表示为( )
| A. | 10×106 | B. | 1×108 | C. | 1000×104 | D. | 1×107 |
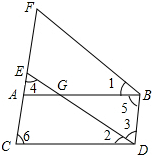 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据. 如图,在等腰Rt△ABC中,∠B=90°,BC=BA=6,D为AC上任意一点,把△CDB绕B点逆时针旋转90°,补充完旋转后的图形,并求出把△CDB旋转后所得的三角形与△ABD的面积之和.
如图,在等腰Rt△ABC中,∠B=90°,BC=BA=6,D为AC上任意一点,把△CDB绕B点逆时针旋转90°,补充完旋转后的图形,并求出把△CDB旋转后所得的三角形与△ABD的面积之和.