题目内容
15.已知二次函数y=ax2-bx+c(a≠0),其图象经过A(3-m,2),B(m+1,2)两点,则$\frac{b}{a}$的值为( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
分析 利用二次函数y=ax2-bx+c(a≠0)的对称轴x=$-\frac{-b}{2a}$,由二次函数y=ax2-bx+c的图象经过两点(3-m,2)、(m+1,2),由这两点的纵坐标相等,即可得这两点关于对称轴对称,即可求得对称轴方程x=$\frac{3-m+m+1}{2}$,可得$\frac{b}{a}$.
解答 解:∵二次函数y=ax2-bx+c的图象经过两点(3-m,2)、(m+1,2),
∴对称轴方程x=$\frac{3-m+m+1}{2}$=$-\frac{-b}{2a}$,
∴$\frac{b}{2a}=2$,
∴$\frac{b}{a}=4$,
故选C.
点评 此题考查了二次函数点的对称性.题目比较简单,解题的关键是注意审题,理解题意,根据函数的对称性解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列四个数中,正整数是( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
7. 如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )
如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )
 如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )
如图,在平面内直角坐标系中,直线l:y=$\frac{\sqrt{3}}{3}$x+1交x轴于点A,交y轴于点B,点A1,A2,A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则OAn的长是( )| A. | 2n$\sqrt{3}$ | B. | (2n+1)$\sqrt{3}$ | C. | (2n-1-1)$\sqrt{3}$ | D. | (2n-1)$\sqrt{3}$ |
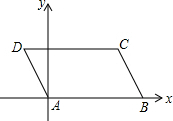 如图,在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,建立如图所示的平面直角坐标系,试分别求出B,C,D三点的坐标.
如图,在?ABCD中,AB=5,AD=2,∠DAB=120°,若以点A为原点,直线AB为x轴,建立如图所示的平面直角坐标系,试分别求出B,C,D三点的坐标.