题目内容
5.先化简,再求值:($\frac{4a-b}{a+b}$-$\frac{b}{a-b}$)÷$\frac{3b-2a}{a+b}$,其中a=2,b=3.分析 根据分式的减法和除法可以化简题目中的式子,然后将a、b的值代入化简后的式子即可解答本题.
解答 解:($\frac{4a-b}{a+b}$-$\frac{b}{a-b}$)÷$\frac{3b-2a}{a+b}$
=$\frac{(4a-b)(a-b)-b(a+b)}{(a+b)(a-b)}×\frac{a+b}{3b-2a}$
=$\frac{2a(2a-3b)}{(a+b)(a-b)}×\frac{a+b}{3b-2a}$
=$-\frac{2a}{a-b}$,
当a=2,b=3时,原式=$-\frac{2×2}{2-3}=4$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
16.在平面直角坐标系中,△ABC的三个顶点分别为A(-4,3),B(-6,1),C(-1,1),将△ABC绕着原点O顺时针旋转180°后得到△A1B1C1,则点B的对应点B1的坐标是( )
| A. | (1,-1) | B. | (4,-3) | C. | (-1,-1) | D. | (6,-1) |
13.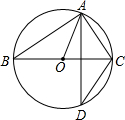 如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )
 如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )
如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )| A. | 64° | B. | 58° | C. | 68° | D. | 55° |
17.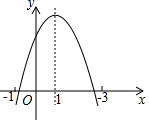 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①b2-4ac=0;②2a+b=0;③若(x1,y1),(x2,y2)在函数图象上,当x1<x2时,y1<y2;④a-b+c<0.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①b2-4ac=0;②2a+b=0;③若(x1,y1),(x2,y2)在函数图象上,当x1<x2时,y1<y2;④a-b+c<0.其中正确的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①b2-4ac=0;②2a+b=0;③若(x1,y1),(x2,y2)在函数图象上,当x1<x2时,y1<y2;④a-b+c<0.其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①b2-4ac=0;②2a+b=0;③若(x1,y1),(x2,y2)在函数图象上,当x1<x2时,y1<y2;④a-b+c<0.其中正确的是( )| A. | ②④ | B. | ③④ | C. | ②③④ | D. | ①②④ |
14. 如图,AB是⊙O直径,若∠D=30°,则∠AOE的度数是( )
如图,AB是⊙O直径,若∠D=30°,则∠AOE的度数是( )
 如图,AB是⊙O直径,若∠D=30°,则∠AOE的度数是( )
如图,AB是⊙O直径,若∠D=30°,则∠AOE的度数是( )| A. | 30° | B. | 60° | C. | 100° | D. | 120° |
15.-2的绝对值是( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | ±2 | D. | 2 |
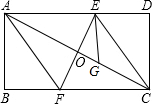 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE;过点E作EG⊥AD交AC于点G.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE;过点E作EG⊥AD交AC于点G.